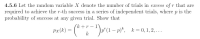
Let the random variable X denote the number of trials in ecess of r that are ed to achieve the r-th success in a series of independent trials, where p is the pility of success at any given trial. Show that
Angles in Circles
Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.
Arcs in Circles
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
My question is attached.
Given that,
The random variable X as the number of trails in excess of r that are required to achieve the r-th success.
The probability of success for given trail is p and the probability of failure is 1-p.
Let us consider, the first success, r=1
P(X=0)=p
P(X=1)=p(1-p)
P(X=2)= p(1-p)2 and so on….
Let us consider, the second success, r=2
P(X=0)=p2
P(X=1)=2p2(1-p)
P(X=2)=3p2(1-p)2 and so on….
Let us consider, the r-th success,
P(X=0)=pr
P(X=1)=rpr(1-p)
P(X=2)=[(r+1)r/2]p2(1-p)2 and so on….
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images
