A cycle starts with an adiabatic compression of the air from state a with a volume V3 to state b with volume V1. At the end of the compression, heat is added (absorbed), resulting in an isobaric expansion to state c with volume V2 followed by an adiabatic expansion back to volume V3 at state d. Finally, heat is expelled, corresponding to an isochoric reduction completing the cycle and bringing air back to state a.
The ratio between the initial and final temperatures for the adiabatic compression is Ta / Tb = 1 / rcγ-1, and the adiabatic expansion is Tc / Td = reγ-1, where the compression ratio rc = V3 /V1 and the expansion ratio re = V3 /V2.
Show that the efficiency of this engine, which only relies on the expansion and compression ratios, is as proved as in figure 1.
.
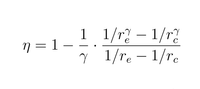
Step by step
Solved in 3 steps with 1 images
