Reese thinks peanut butter and chocolate are great when separate, but when they combine they are even more epic. In other words, Reese likes to eat either peanut butter or chocolate, but when he eats them together, he gets additional satisfaction from the combination. His preference over peanut butter (x) and chocolate (y) is represented by the utility functionz; u(x, y) =
Reese thinks peanut butter and chocolate are great when separate, but when they combine they are even more epic. In other words, Reese likes to eat either peanut butter or chocolate, but when he eats them together, he gets additional satisfaction from the combination. His preference over peanut butter (x) and chocolate (y) is represented by the utility functionz; u(x, y) =
Chapter1: Making Economics Decisions
Section: Chapter Questions
Problem 1QTC
Related questions
Question
Reese thinks peanut butter and chocolate are great when separate, but when they combine they are even more epic. In other words, Reese likes to eat either peanut butter or chocolate, but when he eats them together, he gets additional satisfaction from the combination. His preference over peanut butter (x) and chocolate (y) is
represented by the utility functionz;
u(x, y) = xy + x + y
Suppose now that Reese’s income is high relative to the
chocolate (more concretely, imagine I > px and I > py). What is Reese’s Marshallian
demand for peanut butter, x^∗(Px, Py, I)?
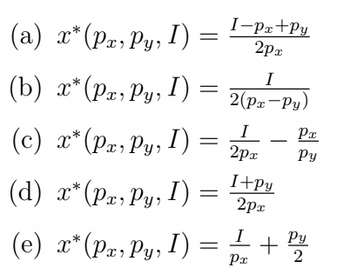
Transcribed Image Text:The image contains a series of equations labeled (a) through (e). Each equation expresses the variable \( x^*(p_x, p_y, I) \) in terms of the variables \( p_x \), \( p_y \), and \( I \). These variables are typically used in economic models where \( p_x \) and \( p_y \) are prices of goods, and \( I \) is income. Here is the transcription of the equations:
(a) \( x^*(p_x, p_y, I) = \frac{I - p_x + p_y}{2p_x} \)
(b) \( x^*(p_x, p_y, I) = \frac{I}{2(p_x - p_y)} \)
(c) \( x^*(p_x, p_y, I) = \frac{I}{2p_x} - \frac{p_x}{p_y} \)
(d) \( x^*(p_x, p_y, I) = \frac{I + p_y}{2p_x} \)
(e) \( x^*(p_x, p_y, I) = \frac{I}{p_x} + \frac{p_y}{2} \)
Each equation depicts a different functional form, likely evaluating the optimal choices given the specified constraints and parameters.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps
Recommended textbooks for you
Principles of Economics (12th Edition)
Economics
ISBN:
9780134078779
Author:
Karl E. Case, Ray C. Fair, Sharon E. Oster
Publisher:
PEARSON
Engineering Economy (17th Edition)
Economics
ISBN:
9780134870069
Author:
William G. Sullivan, Elin M. Wicks, C. Patrick Koelling
Publisher:
PEARSON
Principles of Economics (12th Edition)
Economics
ISBN:
9780134078779
Author:
Karl E. Case, Ray C. Fair, Sharon E. Oster
Publisher:
PEARSON
Engineering Economy (17th Edition)
Economics
ISBN:
9780134870069
Author:
William G. Sullivan, Elin M. Wicks, C. Patrick Koelling
Publisher:
PEARSON
Principles of Economics (MindTap Course List)
Economics
ISBN:
9781305585126
Author:
N. Gregory Mankiw
Publisher:
Cengage Learning
Managerial Economics: A Problem Solving Approach
Economics
ISBN:
9781337106665
Author:
Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike Shor
Publisher:
Cengage Learning
Managerial Economics & Business Strategy (Mcgraw-…
Economics
ISBN:
9781259290619
Author:
Michael Baye, Jeff Prince
Publisher:
McGraw-Hill Education