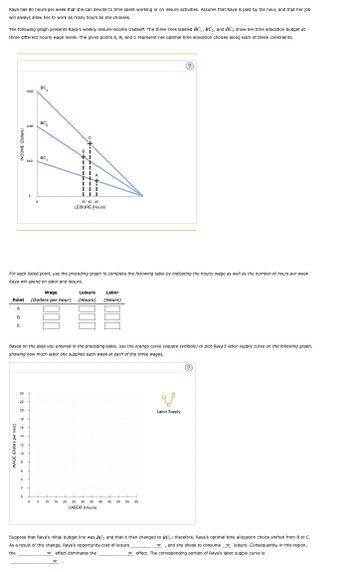
Raya has 80 hours per week that she can devote to time spent working or on leisure activities. Assume that Raya is paid by the hour, and that her job will always allow her to work as many hours as she chooses. The following graph presents Raya's weekly leisure-income tradeoff. The three lines labeled BC, BC, and BC, show her time allocation budget at three different hourly wage levels. The given points A, B, and C represent her optimal time allocation choices along each of these constraints. 1920 BC3 1280 BC₂ 640 BC₁ 5 0 35 40 45 LEISURE (Hours) For each listed point, use the preceding graph to complete the following table by indicating the hourly wage as well as the number of hours per week Raya will spend on labor and leisure. Point Wage (Dollars per hour) (Hours) Leisure Labor (Hours) A B C Based on the data you entered in the preceding table, use the orange curve (square symbols) to plot Raya's labor supply curve on the following graph, showing how much labor she supplies each week at each of the three wages. 24 22 20 18 16 14 12 10 6 4 2 0 + 0 5 10 15 20 25 30 35 40 45 50 55 60 LABOR (Hours) Labor Supply Suppose that Raya's initial budget line was BC, and that it then changed to BC; therefore, Raya's optimal time allocation choice shifted from B to C. As a result of this change, Raya's opportunity cost of leisure the effect dominates the , and she chose to consume ▼lelsure. Consequently, in this region, effect. The corresponding portion of Raya's labor supply curve is

Solve it

Emberlynn has 80 hours per week that she can devote to time spent working or on leisure activities. Assume that Emberlynn is paid by the hour, and that her job will always allow her to work as many hours as she chooses. The following graph presents Emberlynn's weekly leisure-income tradeoff. The three lines labeled BC₁, BC₂, and BC show her time allocation budget at three different hourly wage levels. The given points A, B, and C represent her optimal time allocation choices along each of these constraints. INCOME (Dollars) 1200 800 400 0 BC₂ 8 BC, C 35 40 45 LEISURE (Hours) For each listed point, use the preceding graph to complete the following table by indicating the hourly wage as well as the number of hours per week Emberlynn will spend on labor and leisure. Wage Leisure Labor Point (Dollars per hour) (Hours) (Hours) A B C

Please show the exact plotting points for the graph and please answer the table and last question