
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
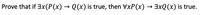
Transcribed Image Text:**Title:** Logical Implication Proof
**Objective:** Prove that if ∃x(P(x) → Q(x)) is true, then ∀xP(x) → ∃xQ(x) is true.
**Explanation:**
The given problem involves proving the logical implication between two quantified statements:
1. **Existential Quantifier → Implication Statement:**
- ∃x(P(x) → Q(x)): There exists at least one x such that if P(x) is true, then Q(x) is also true.
2. **Universal Quantifier → Existential Implication Statement:**
- ∀xP(x) → ∃xQ(x): If P(x) is true for all x, then there exists an x such that Q(x) is true.
**Proof Strategy:**
- Assume ∃x(P(x) → Q(x)) is true, which means there is at least one specific instance (let's call it x₀) where P(x₀) implies Q(x₀).
- To show ∀xP(x) → ∃xQ(x), consider:
- If ∀xP(x) is true, that means P is true for every instance.
- Since we already have an x₀ where P(x₀) → Q(x₀) is true, and P(x₀) is true (because ∀xP(x)), Q(x₀) must also be true.
- Therefore, ∃xQ(x) is satisfied by x₀.
This logical reasoning shows that the initial assumption leads us to the conclusion that ∀xP(x) → ∃xQ(x) is indeed true whenever ∃x(P(x) → Q(x)) is true.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Find the simplest POS expression using K- Maps for the following functions. For each, list all prime implicants found in the K-Map, then list only the essential prime implicants, and then list the simplest solution. i. f (x1, x2, x3) = II M (0, 1, 2, 4, 5) ii. f (x1,x2, x3, x4) = ПМ (0, 1, 2,4, 5) Em (1, 2,5, 6, 7,8, 10, 14)arrow_forwardThis is a practice problem I need help with.arrow_forwardUsing k-map..arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education