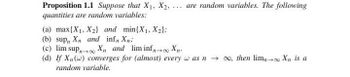
Proposition 1.1 Suppose that X1, X2,... are random variables. The following quantities are random variables: (a) max{X1, X2) and min(X1, X2); (b) sup, Xn and inf, Xn; (c) lim sup∞ X and lim inf∞ Xn- (d) If Xn(w) converges for (almost) every w as n→ ∞, then lim- random variable. → Xn is a

Example 2: Let X1, X2, X10 be independent random variables with a common uniform distribution over the interval (0, 1). Estimate P[Σ],X; < 6].

2. Let U1, U2,... be independent random variables, each with continuous distribution that is uniform in the interval [-3, 3]. Let S, = U ++ Un. (a) Compute the moment generating function of U1. (b) Compute the moment generating function of S,. (c) Determine E(S) and E(S) (by any method).

Section II 11. Assume X is a random variable with moment generating function M(t) (0.3et +0.7), -0

Suppose X1, X2, ... , Xn is a random sample and Xi = {1, with probability p         0, with probability 1-p} for every i = 1, 2, ... , n.   Find the Moment Generating Function of ∑i=1n Xi . What is the distribution of ∑i=1n Xi ?

Let X and Y be independent random variables taking non-negative integer values, having probability generating functions 1 1 for s < 2 (for X) and (2-9 for s < 2 (for Y). (2– s)2 (2 – s)4 Calculate E((X +Y)²).

9- A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. Let X = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of X is i) f(x) = { = { kd² 0 the value of k and draw th Total kx² 0≤x≤2 otherwise LE COR v) What is the expected value of X? vi) what is the variance of X? curve. [Hint: anilll Ul UlIC - Jocture continues for at 1

A particle is confined in a straight tunnel aligned in east-west direction and it can move randomly by the step size of one or two units. For each movement, the probability is p that the particle will move one unit to the west, the probability is q that the particle will move two units to the east, and the probability is 1 – p – q that the particle will remain at the same place. (0 < p < 1,0 < q < 1,0 < 1- p – q < 1). A movement is independent to another. Calculate the expectation of the position of the particle after n movements, assuming that the position of starting point is 0.

Please solve (c) & (d) only!

3.) Suppose X has probability generating function GX(t) = 0.2 + 0.3t + 0.1t2 + 0.4t3. What is P(X = 2)? What is P(X = 0)?