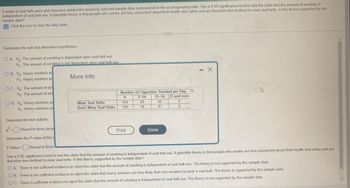
A study of seat belt users and nonusers yielded the randomly selected sample data summarized in the accompanying table. Use a 0.05 significance level to test the claim that the amount of smoking is independent of seat belt use. A plausible theory is that people who smoke are less concerned about their health and safety and are therefore less inclined to wear seat belts. Is this theory supported by the sample data? Click the icon to view the data table. Determine the null and alternative hypotheses. OA. Ho: The amount of smoking is dependent upon seat belt use. H₁: The amount of smoking is not dependent upon seat belt use. OB. Ho: Heavy smokers an H₁: Heavy smokers an OC. Ho: The amount of sm H₁: The amount of sm OD. Ho Heavy smokers an H₁: Heavy smokers ar Determine the test statistic. x²= (Round to three decin More Info Number of Cigarettes Smoked per Day 0 1-14 15-34 35 and over Wear Seat Belts 193 20 42 9 Don't Wear Seat Belts 159 10 41 9 Determine the P-value of the t P-Value = (Round to three Print Done - X Use a 0.05 significance level to test the claim that the amount of smoking is independent of seat belt use. A plausible theory is that people who smoke are less concerned about their health and safety and are therefore less inclined to wear seat belts. Is this theory supported by the sample data? OA. There is not sufficient evidence to reject the claim that the amount of smoking is independent of seat belt use. The theory is not supported by the sample data. OB. There is not sufficient evidence to reject the claim that heavy smokers are less likely than non-smokers to wear a seat belt. The theory is supported by the sample data. O C. There is sufficient evidence to reject the claim that the amount of smoking is independent of seat belt use. The theory is not supported by the sample data. 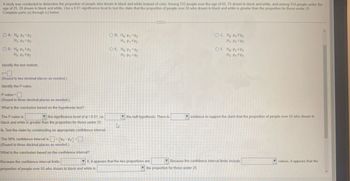A study was conducted to determine the proportion of people who dream in black and white instead of color. Among 312 people over the age of 55, 75 dream in black and white, and among 314 people under the age of 25, 20 dream in black and white. Use a 0.01 significance level to test the claim that the proportion of people over 55 who dream in black and white is greater than the proportion for those under 25. Complete parts (a) through (c) below. OA. Ho P1 P2 H₁ P1 P2 OD. Ho P1 P2 H₁ P1 P2 Identify the test statistic. z= OB. Ho P1 P2 H₁ P1 P2 OC. Ho P1 P2 H₁ P1 P2 OF. Ho P₁ SP2 OE. Ho P1 P2 H₁ P1 P2 H₁: P1 P2 (Round to two decimal places as needed.) Identify the P-value. P-value = (Round to three decimal places as needed.) What is the conclusion based on the hypothesis test? The P-value is the significance level of a = 0.01, so black and white is greater than the proportion for those under 25. b. Test the claim by constructing an appropriate confidence interval. The 98% confidence interval is < (P1 P2) < (Round to three decimal places as needed.) What is the conclusion based on the confidence interval? Because the confidence interval limits proportion of people over 55 who dream in black and white is 13 the null hypothesis. There is evidence to support the claim that the proportion of people over 55 who dream in 0, it appears that the two proportions are Because the confidence interval limits include the proportion for those under 25. values, it appears that the

The cash register receipts each day last week at a coffee shop were $1,845. $1,520. $1,438, $1,682, $1,850, $2,721, $2,539. Find the (a) mean, (b) median, and (c) mode.