
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
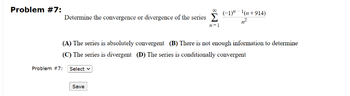
Transcribed Image Text:Problem #7:
Determine the convergence or divergence of the series >
n=1
Problem #7:
(A) The series is absolutely convergent (B) There is not enough information to determine
(C) The series is divergent (D) The series is conditionally convergent
Select
(-1)-¹(n+914)
Save
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 4 images

Knowledge Booster
Similar questions
- 4. Determine if the series is absolutely convergent, conditionally convergent, or divergent using one of the following (divergence test, integral test, comparison test, limit comparison test, alternating series test, ratio test, root test).arrow_forwardAn environmental engineer wants to evaluate three different methods for disposing of nonhazardous chemical waste: land application, fluidized-bed incineration, and private disposal contract. Use the estimates below to help her determine which has the least cost at /= 15.00% per year on the basis of an annual worth evaluation. First Cost AOC per Year Salvage Value Life Land $-145000 $-86000 $23000 4 years Incineration $-760000 $-70000 $260000 6 years Contract O $-132000 O 2 yearsarrow_forward12. Determine if the series is absolutely convergent, conditionally convergent, or divergent using one of the following (divergence test, integral test, comparison test, limit comparison test, alternating series test, ratio test, root test).arrow_forward
- 7. Evaluate the series (-2)k+1 32k-1 k=2 8 8 2 3 3 (a) (b) 21 33 9 6 6 4 (e) (f) 7 11 (i) The series is convergent, but not equal to any of these answers. 8 45 (h) 4 (j) The series is divergent. (d)arrow_forwardProblem 1. The Alternating Series Test states that if the positive sequence {b„} is (1) decreasing, and (2) convergent to 0, then the series > (-1)"+'bn converges. But what if we drop the assumption that {bn} is decreasing? Is the n=1 result still true? Consider the series defined by 1 1 1 1 1 1 1 1 (-1)"+1bn, - 2 4 3 8. 4 16 2n n=1 where the sequence b, is defined by 1 1 1 1 1 1 1 4' 3'8'4'16’5'32' 1 1 } n 2n (a) Does this sequence {bn} satisfy the assumptions of the Alternating Series Test? Which does it satisfy, and which does it fail? 1 (b) Show that this series diverges. (Hint: This series can also be written as Suppose that it did n 2n n=1 should converge. If you add a certain geometric series to it, you're adding two convergent series together, so you get another convergent series but do you?) (c) Is the Alternating Series Test wrong? Explain why not.arrow_forwardFor problem 2 part 2: To get your comparison series for LCT, choose the series with leading term over leading term. So you want the series of sqrt{n} over n "leading term over leading term" then go from therearrow_forward
- 1. If the series an is convergent and an > 0 for all n, then we also know that n=1 (a) Must be Convergent (b) Must be Divergent (c) Can be either Convergent or Divergent, depending on an M8 n=1 an n Earrow_forward∞ 1. Let an be a POSITIVE infinite series (i.e. an > 0 for all n ≥ 1). Let ƒ be a continuous function n=1 with domain R. Is each of these statements true or false? If it is true, prove it. If it is false, prove it by providing a counterexample and justify that is satisfies the required conditions.arrow_forwardAQuestion Completion Status: Problem 1: Which of the following series converge by the alternating series test. Select all that apply. (-1)"n² 回》 Vn3 + 1 n=1 8 [ii] (-1)"-!el-n n=1 (-1)" [iii] ) 2+3n n=1 [iv] (-1)"n In(n) n=1 [i] [ii] [iv] Save All Answers Close Window Click Save and Submit to save and submit. Click Save All Answers to save all answers. pg.jpg MATH1132_Q11.2.pdf pg.jpg MATH1132_Q11.4.pdf MATH1132_Q11.3.pdf Essay 1 Makin....docx POF MacBook Proarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

