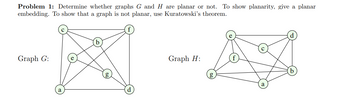
Problem 1: Determine whether graphs G and H are planar or not. To show planarity, give a planar embedding. To show that a graph is not planar, use Kuratowski's theorem. X Graph G: Graph H: b

Instruction: It should be a C++ PROGRAM INCLUDE THE HEADER FILE, MAIN CPP, AND BSTREE.CPP There is a real program developed by a computer company that reads a report ( running text ) and issues warnings on style and partially corrects bad style. You are to write a simplified version of this program with the following features:   Statistics   A statistical summary with the following information: Total number of words in the report Number of unique words Number of unique words of more than three letters Average word length Average sentence length An index (alphabetical listing) of all the unique words (see next page for a specific format)   Style Warnings   Issue a warning in the following cases: Word used too often: list each unique word of more than three letters if its usage is more than 5% of the total number of words of more than three letters Sentence length : write a warning message if the average sentence length is greater than 10 Word length : write a warning message if the…

16 Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar. var num2 = 32; var num1 = 12; var rem=num2 % num1; while(rem> 0) { num2 = num1; num1 = rem; rem =num2 9% num1; document.write(num1): The output of the document.write statement at the end of this block is Reset Next m. All rights reserved. 5896

Please write code that would run in VBA please show code in VBA