
Chemistry
10th Edition
ISBN: 9781305957404
Author: Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Please show work thank you very much.
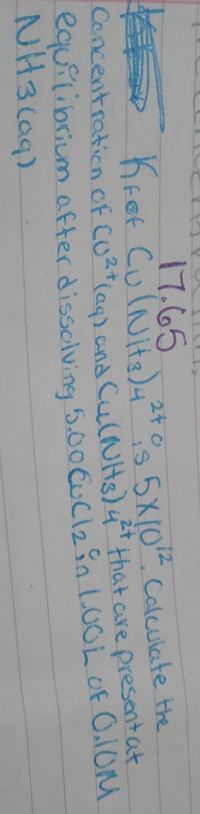
Transcribed Image Text:**Problem Statement:**
Given:
- \( K_f \) for \( \text{Cu(NH}_3\text{)}_4^{2+} \) is \( 5 \times 10^{12} \).
Task:
Calculate the concentration of \( \text{Cu}^{2+} \) (aq) and \( \text{Cu(NH}_3\text{)}_4^{2+} \) that are present at equilibrium after dissolving 5.00 g of \( \text{CuCl}_2 \) in 1.00 L of 0.10 M \( \text{NH}_3 \) (aq).
**Solution Outline:**
1. Understand the dissociation and complexation reactions involved:
- \( \text{CuCl}_2 \) dissolves to form \( \text{Cu}^{2+} \).
- \( \text{Cu}^{2+} \) reacts with \( \text{NH}_3 \) to form \( \text{Cu(NH}_3\text{)}_4^{2+} \).
2. Calculate initial moles of each reactant.
3. Use the stability constant \( K_f \) to determine equilibrium concentrations.
4. Apply the ICE table (Initial, Change, Equilibrium) method to solve for unknowns.
Note: Detailed calculations would follow the standard steps in equilibrium chemistry involving setting up appropriate expressions for \( K_f \) and solving for equilibrium concentrations.
Expert Solution
arrow_forward
Step 1-Introduction
In an equilibrium reaction, the rate of formation of the products is equal to the rate of their disappearance. There should not be any notable change in the composition of the participating components of the medium.
So the concentration of the species present at equilibrium is expressed as the ratio of the concentration of products to the reactant species concentration. Mathematically, the equilibrium constant () for a reaction is furnished as follows:
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- 1 match Begins with : Q Gently insert the c Done Messages Courses Help Spring 2022 CHEM 106 Mengting Wu ▼ (Student - section: C54) Logou Main Menu Contents Grades Groups Course Timer Notes Evaluate Feedback Print Inf Follow proper technique when using a pipet: False A volumetric pipet should 'not be "blown out" to eject all liquid at the tip. Volumetric pipets are calibrated in a manner that takes into account the solution which remains at the tip. True Using the pipettor, you should turn the wheel on the pipette, draw up the solution until the meniscus is several centimeters above the calibration line, then quickly remove the pipette and put your thumb over the open hole of the pipet. True When the bottom of the meniscus coincides with the calibration mark, your pipet contains a precisely measured volume. True e Do not force the pipet into the pipettor, be gentle. Excessive force may cause the pipet to break and could potentially cut you while trying to insert or remove the pipet.…arrow_forwardChrome File Edit View History Bookmarks Profiles Tab Window Help A 84% Wed 8:14 T WPAL 101_ 233 _Spring 2022 O NEW BEST Builder Hall 5 Base x ALEKS - David Teague - Learn x X Grades for David Teague: CHM A www-awu.aleks.com/alekscgi/x/lsl.exe/1o_u-IgNslkr7j8P3jH-IVDWKW_BBZZI6tTytly4Fcfu6zOtOf80MM9sfGh3NIP72XeoPmXkrk4zqM9ylm-ZZhvViL. O ☆ D Paused O CHEMICAL REACTIONS David Writing a chemical equation from a description of the reaction 2/5 Aqueous potassium nitrate (KNO3) and solid silver bromide are produced by the reaction of aqueous potassium bromide and aqueous silver nitrate (AgNO,). Write a balanced chemical equation for this reaction.arrow_forward2- 3. Ch4 - Mastery Gmail с !!! X Canvas OWLv2 | Online teaching and l X docs.google.com/document/d/1TqDL3pNyiUclZ_7MKQ6brZDQFIAmOD1jfbX4SLstrel/edit Rangermail P University of Wisc... a se a A 100% Untitled document File Edit View Insert Format Tools Extensions Help 1 Normal text H Quizlet C chegg Verdana H I H₂N. I CI 1 I Untitled document - Google D X b Success Confirmation of Ques x + CH3 H I H 11.5 + H. H GPT P Student Center 2 -NH₂ Note that cis, trans isomers are an example of stereoisomers. Indicate whether the pair of structures shown represent stereoisomers, constitutional isomers, different conformations of the same compound, or the same conformation of a compound viewed from a different perspective. H CH3 H₂N- B I U A H I CI 3 ين - 4 Moncler NH₂| C + Pearson+ Public S... d = = ▶ Geo Book E Cengage Ochem 1 E EX 0 О н Update: ✓ Editing Share Harrow_forward
- A mixer was purchased two yearsago for $ 60726 and can be sold for$125,000 today. The mixer has beendepreciated using the MACRS 5-yearrecovery period and the firm pays 40 percent taxes on both ordinaryincome and capital gain. Find thebook value.arrow_forwardThe The O Cont Full Enha Dash MISS C Assu B The C This O Effec 5 Mc G syml college.com/course.html?courseld316985674&OpenVellumHMAC=Dad585d15954695d5b7068f8de43c2850#10001 View Available Hint(s) V2 = L Submit < Return to Assignment Provide Feedback 7:03 PM 76°F Partly cloudy 12/12/2021 19 rch 56 BHJC04Z022B01 E7arrow_forwardChrome File Edit View History Bookmarks Profiles Tab Window Help → C My Shelf | RedShelf Chapter 9 ppt - af X Part A >> rian's na's webp lease dfarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY

Chemistry
Chemistry
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning

Chemistry
Chemistry
ISBN:9781259911156
Author:Raymond Chang Dr., Jason Overby Professor
Publisher:McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:9781305577213
Author:Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:Cengage Learning

Organic Chemistry
Chemistry
ISBN:9780078021558
Author:Janice Gorzynski Smith Dr.
Publisher:McGraw-Hill Education

Chemistry: Principles and Reactions
Chemistry
ISBN:9781305079373
Author:William L. Masterton, Cecile N. Hurley
Publisher:Cengage Learning

Elementary Principles of Chemical Processes, Bind...
Chemistry
ISBN:9781118431221
Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:WILEY