Now suppose we are dealing with a Non-Newtonian material such as baking dough, say. We must specify a constitutive relation for this material; note that the following expression has a nonlinear term: σij ​=2μeij ​+α(eij eij​ ) a. Calculate the components of σij ​for baking dough undergoing this simple shearing motion. b. Determine the components of the traction vector t on the top plate (where t =σ. n and represents the force per unit area exerted by the plate on the baking dough. 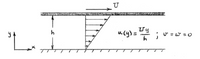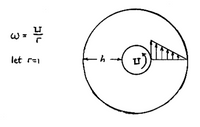Note that we are ignoring the static contribution in the last expression.) c. Note that a flow as sketched in Fig. 2 below can be closely approximated by a Couette flow. Therefore, use the results of part b to explain why baking dough tends to rise up the shaft of a mixer. d. Would your explanation still hold if baking dough were a

Refer to Figure Q2. A tray of mass mı is supported by 3 springs as shown in Figure 3(a). The natural frequency fa is 5.0Hz. An additional mass motor of m2 = 3.0kg (in OFF condition) is placed at the center on top of the mass, the natural frequency is observed to be 2.5Hz. a) Calculate the mass mı. The motor m2 is ON and it rotates at the speed of 600 rpm. Calculate: a) The transmissibility b) Attenuation c) Explain what will happen if the system run at Resonant Frequency m2 m1 Figure 2(a): Original system Figure 2(b): system with m2 added

Consider the following spring system. Assume down is the positive direction. Write the stiffness matrix A 188 Displacement www my SE (₂ • Compute the displacements caused by the external forces f with spring constants e E

A spring connects mass m of a pendulum to a wall as shown in the figure. The original un- stretched length of the spring is L. Use the Energy Method and find the equation of motion of the system in terms of the angle 0. L L K m Original Length = L

See the attached image1) A long rod in the shape of a circular cone is rotating with constant angular velocity c about an axis located at the left end of the rod as shown in the figure below. The bar has length L, major and minor diameters D and d, respectively, and its material has linear elastic behavior with modulus of elasticity E. The values of the problem parameters must be defined by the student a) From the balance of a differential member of the bar, derive the differential equation of balance for the bar. Solve the equation analytically to obtain the bar displacement field, U(X). Give the expression for the displacement at the free end of the member. b) Implement a computational code in MATLAB (or any other software) to solve this problem with "n" two-node bar finite elements. c) Run different simulations by increasing the number of finite elements in each simulation. At each simulation, obtain the displacement of the free end of the member. Graphically compare your results…

Please show the work to understand the process. AI generated steps have been wrong.

Can you please show the complete solution and free body diagram of the image below. Thanks! Subject: Mechanical Vibration

7. The arrangement in the drawing shows a block (mass = 14.0 kg) that is held in position on a frictionless incline by a cord (length = 0.582 m). The mass per unit length of the cord is 1.30 x 10-2 kg/m, so the mass of the cord is negligible compared to the mass of the block. The cord is being vibrated at a frequency of 166 Hz (vibration source not shown in the drawing). What is the smallest angle 0 between 15.0° and 90.0° at which a standing wave exists on the cord?

III) A relatively well-praised model for a car suspension is depicted in Figure 5: 4 4 Body Mass MW Suspension Mass b₂ ↑" Figure 5 - Model of the suspension of a car. Considering it is a system with two degrees of freedom, WRITE the equations that model the free vibrations of this system.

Consider the spring assemblage shown, using the direct stiffness method do the following: 1. Write the global stiffness matrix 2. Determine the nodal displacements 3. Determine the nodal forces 4. Determine the reaction of supports K1 = 15 kN/m f Node 1 F = 0.675 kN K2 = 45 kN/m No Node 2 X positive to the right vov Node 3 K3 = 15 N/m Node 4