
NEWTON-RAPHSON METHOD
EXAMPLE 1: Find the root of the function ?(?) = cos (?) using NRM having initial approximation of 1
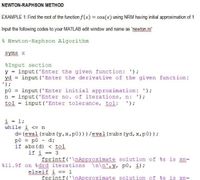
Input the following codes to your MATLAB edit window and name as “newton.m”
% Newton-Raphson
syms x
%Input section
y = input('Enter the given function: ');
yd = input('Enter the derivative of the given function:
');
p0 = input('Enter initial approximation: ');
n = input('Enter no. of iterations, n: ');
tol = input('Enter tolerance, tol: ');
i = 1;
while i <= n
d=(eval(subs(y,x,p0)))/eval(subs(yd,x,p0));
p0 = p0 - d;
if abs(d) < tol
if i == 3
fprintf('\nApproximate solution of %s is xn=
%11.9f on %drd iterations \n\n',y, p0, i);
elseif i == 1
fprintf('\nApproximate solution of %s is xn=
%11.9f on %dst iterations \n\n',y, p0, i);
elseif i == 2
fprintf('\nApproximate solution of %s is xn=
%11.9f on %dnd iterations \n\n',y, p0, i);
else
fprintf('\nApproximate solution of %s is xn=
%11.9f on %dth iterations \n\n',y, p0, i);
end
break;
else
i = i+1;
end
end
Run the program and enter the following.
Enter the given function: cos(x)
Enter the derivative of the given function: -sin(x)
Enter initial approximation: 1
Enter no. of iterations, n: 30
Enter tolerance, tol: 0.0001
Write the output below:

Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 1 images

- Using matlabarrow_forwardCan you help me write the code for this MATLAB assignment?arrow_forwardQ3: Write a matlab program call matq3.m that returns the plot of the 2- D space defined by the following equation: (-xsin(x) cos (x) - 2π ≤ x < 0 x ≥ 2π Label the x-axis and y-axis and z-axis and title to the curve. y =arrow_forward
- Here are three versions of a code fragment located inside a function: Version A for Row in range(10): for Column in range(5): DoSomethingInteresting(Row,Column) return Version B for Row in range(10): for Column in range(5): DoSomethingInteresting(Row,Column) return Version C for Row in range(10): for Column in range(5): DoSomethingInteresting(Row,Column) return How many times do each of the versions call the DoSomethingInteresting function? Write a sentence or two explaining which version is the "correct" versionarrow_forwardanswer with matlab code. do not use aiarrow_forwardMatlab Questionarrow_forward
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY





