MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Question
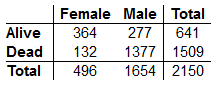
Newspaper headlines at the time and traditional wisdom in the succeeding decades have held that women and children escaped a sunken ship in greater proportion than men. Here's a table with the relevant data. Do you think that survival was independent of whether the person was male or female? Defend your conclusion.
A. Is there evidence of a significant difference between the proportion of males and females who survived at the 0.005 level of significance? What are the null and alternative hypotheses to test?
B. Are the conditions for inference satisfied?
C. Calculate the test statistic
D. Determine the P-value and interpret the meaning
E. Reject or Fail to Reject and why?
Transcribed Image Text:This table presents a summary of survival data differentiated by gender. It consists of two main categories: "Alive" and "Dead," with subtotals provided for each gender as well as an overall total. Here's a detailed breakdown:
- **Alive**
- **Female:** 364
- **Male:** 277
- **Total Alive:** 641
- **Dead**
- **Female:** 132
- **Male:** 1,377
- **Total Dead:** 1,509
- **Grand Total**
- **Female Participants:** 496
- **Male Participants:** 1,654
- **Overall Total Participants:** 2,150
The table clearly indicates the gender distribution in terms of survival outcomes within the given dataset.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 7 images
Knowledge Booster
Similar questions
- A newsletter publisher believes that over 33% of their readers own a Rolls Royce. For marketing purposes, a potential advertiser wants to confirm this claim. After performing a test at the 0.10 level of significance, the advertiser failed to reject the null hypothesis. What is the conclusion regarding the publisher's claim? Answer There is sufficient evidence at the 0.10 level of significance that the percentage is over 33%. There is not sufficient evidence at the 0.10 level of significance to say that the percentage is over 33%arrow_forwardRead through this scenario and look at the data that was collected. State the null and all possible research hypotheses. Review the results below (I used SPSS) and answer the questions that follow. Scenario: A researcher wants to see if gender and / or income affects the total amount of help given to a stranger who is sitting on the side of a busy road with a sign asking for help. The independent variables are gender, income, and the interaction of gender and income. The dependent variable is total help. He wants to know if one or both factors – or the interaction of the two - affects the total amount of help offered. Because he is analyzing two independent variables (gender and income), he used a factorial ANOVA. His results show the main effect of each of the independent variables on the dependent variable (total help) and the interaction effect. The researcher is using a 95% confidence interval which means that he wants to be at least 95% sure that his independent variables…arrow_forwardA study was done using a treatment group and a placebo group. The results are shown in the table. Assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. Complete parts (a) and (b) below. Use a 0.05 significance level for both parts. a. Test the claim that the two samples are from populations with the same mean. What are the null and alternative hypotheses? O A. Ho: M#H2 H₁: H₁ H₂ OC. Ho: H1arrow_forwardThe standard error for is equal to 0.113. The test statistic for the hypothesis test specified in question 9 is equal to:arrow_forwardIn general, if sample data are such that the null hypothesis is rejected at the ? = 1% level of significance based on a two-tailed test, is H0 also rejected at the ? = 1% level of significance for a corresponding one-tailed test? Explain your answer. Yes. If the two-tailed P-value is smaller than ?, the one-tailed area is also smaller than ?. No. If the two-tailed P-value is smaller than ?, the one-tailed area will be larger than ?. Yes. If the two-tailed P-value is smaller than ?, the one-tailed area will be larger than ?. No. If the two-tailed P-value is smaller than ?, the one-tailed area is also smaller than ?.arrow_forwardHello!! I need help with this question! Thank you very mucharrow_forwardTest the claim that the proportion of men who own cats is smaller than the proportion of women who own cats at the .05 significance level. The null and alternative hypothesis would be: Ho: HM = HF H,:PM = PF Ho: HM = PF Ho:HM = Pr Ho:PM = Pr Ho:PM PF H1: HM PF H1:HM > HF H1:HM # HF H1:PM + PF H1:PM < Pf The test is: right-tailed two-tailed left-tailed Based on a sample of 40 men, 40% owned cats Based on a sample of 40 women, 65% owned cats The test statistic is: (to 2 decimals) The p-value is: (to 4 decimals) Based on this we: O Reject the null hypothesis OFail to reject the null hypothesis Check Answerarrow_forward2) If you were interested in testing for a statistical relationship between taking Vitamin A and cold status in the population of elementary school students (i.e.: testing the null hypothesis of no difference in the proportion of colds in Vitamin A and placebo groups, versus the alternative hypothesis of a difference in proportions), the correct statistical test is: a. Two-sample t-test b. Ad-hoc test for testing the equality of things c. Chi-squared test d. Paired t-testarrow_forwardA consumer product testing organization uses a survey of readers to obtain customer satisfaction ratings for the nation's largest supermarkets. Each survey respondent is asked to rate a specified supermarket based on a variety of factors such as: quality of products, selection, value, checkout efficiency, service, and store layout. An overall satisfaction score summarizes the rating for each respondent with 100 meaning the respondent is completely satisfied in terms of all factors. Suppose sample data representative of independent samples of two supermarkets' customers are shown below. Supermarket 1 Supermarket 2 n = 260 n, = 300 = 84 X, = 83 (a) Formulate the null and alternative hypotheses to test whether there is a difference between the population mean customer satisfaction scores for the two retailers. (Let u, = the population mean satisfaction score for Supermarket 1's customers, and let u, = the population mean satisfaction score for Supermarket 2's customers. Enter != for as…arrow_forwardYou’re interested in whether there is a difference in the number of recent stressful life events reported by students at UQ vs. QUT vs. Griffith. The outcome measure was skewed. Which statistical test is appropriate to analyse these data? Friedman’s rank test Kruskal-Wallis test Wilcoxon’s rank-sum test Wilcoxon’s signed-ranks testarrow_forwardI need help with this questionarrow_forwardTest the claim that the proportion of men who own cats is significantly different than the proportion of women who own cats at the 0.02 significance level. The null and alternative hypothesis would be: Ho: M = μF Ho: PM = PF H₁ μM μF H₁:PM > PF The test is: left-tailed right-tailed two-tailed Based on a sample of 60 men, 30% owned cats Based on a sample of 40 women, 45% owned cats The test statistic is: Ho: PM = PF H₁: PM μF (to 2 decimals) (to 2 decimals) Ho: PM = PF Ho: M = μF H₁:PM ‡ PF H₁: μM < MFarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman