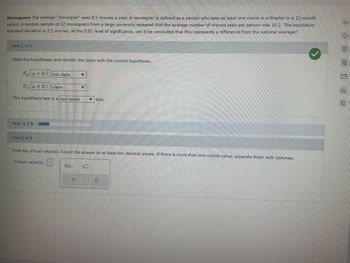
**Title: Understanding Hypothesis Testing in Movie-Going Habits****Introduction:**This educational content explores a hypothesis test concerning the average number of movies watched by moviegoers. A moviegoer is defined as someone who watches at least one movie in a theater over a 12-month period. We examine whether a sample mean differs significantly from a known national average.**Problem Statement:**The average moviegoer sees 8.5 movies per year. A sample of 42 moviegoers from a large university reported an average of 10.2 movies per year. Given a population standard deviation of 3.2 movies, we will perform a hypothesis test at the 0.01 level of significance to determine if this difference is significant.**Part 1 of 5: Stating the Hypotheses**1. **Null Hypothesis (H₀):** μ = 8.5; the average number of movies watched is 8.5.2. **Alternative Hypothesis (H₁):** μ ≠ 8.5; the average number of movies watched is not 8.5.This scenario requires a two-tailed test, which checks if the sample mean is significantly different, either higher or lower, than the population mean.**Part 2 of 5: Critical Values**- To find the critical value(s), calculations must be rounded to at least two decimal places. Should there be multiple critical values, they should be separated by commas.**Note on Graphs/Diagrams:**- This segment does not include specific graphs or diagrams. However, in a typical educational setting, Z-distribution tables or graphs illustrating the two-tailed hypothesis test would be helpful in visualizing the critical regions.This educational example guides students in understanding the process of hypothesis testing using real-world data and statistical reasoning.

Given Sample size n=42, sd=3.2, population mean μ=8.5, level of significance ɑ=0.01

Answered: Moviegoers The average "moviegoer" sees…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

A hypothesis regarding the weight of newborn infants at a community hospital is that the mean is 7.1 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 6.1, 8.1, 9.1, 10.1, 7.1, 11.1, and 12.1 pounds. What is the sample standard deviation?
A marketing researcher wants to estimate the mean amount spent per year ($) on a web site by membership member shoppers. Suppose a random sample of 100 membership member shoppers who recently made a purchase on the web site yielded a mean amount spent of $55 and a standard deviation of $52. Complete parts (a) and (b) below. a. Is there evidence that the population mean amount spent per year on the web site by membership member shoppers is different from $51? (Use a 0.01 level of significance.) State the null and alternative hypotheses. Ho: H (Type integers or decimals. Do not round. Do not include the $ symbol in your answer.) Identify the critical value(s). The critical value(s) is/are (Type an integer or a decimal. Round to two decimal places as needed. Use a comma to separate answers as needed.) Determine the test statistic. The test statistic, 1STAT, is (Type an integer or a decimal. Round to two decimal places as needed.) State the conclusion. Ho. There is evidence that the…
An analyst found that the average amount of money in bank accounts at his/her bank is $2,000 with a standard deviation of $150. What would be the variance?
A marketing researcher wants to estimate the mean amount spent per year ($) on a web site by membership member shoppers. Suppose a random sample of 100 membership member shoppers who recently made a purchase on the web site yielded a mean amount spent of $58and a standard deviation of $55.Complete parts (a) and (b) below. a. Is there evidence that the population mean amount spent per year on the web site by membership member shoppers is different from $51? (Use a 0.01 level of significance.) State the null and alternative hypotheses.
The systolic blood pressure of adults in the USA is nearly normally distributed with a mean of 121 and standard deviation of 16 .Someone qualifies as having Stage 2 high blood pressure if their systolic blood pressure is 160 or higher.c. Stage 1 high BP is specified as systolic BP between 140 and 160. What percentage of adults in the US qualify for stage 1?____%d. Your doctor tells you you are in the 30th percentile for blood pressure among US adults. What is your systolic BP? Round to 2 decimal places.____lbs
light examined data on employment and answered questions regarding why workers separate from their employes. According to the article, the standard deviation of the length of time that women with one job are employed during the first 8 years of their career is 92 weeks. Length of time employed during the first 8 years of career is a left skewed variable. For that variable, do the following tasks. A. determine the sampling distribution of the sample mean for simple random samples of 50 women with one job. Explain your reasoning B. Obtain the probability that the sampling error made in estimating the mean length of time employed by all women with one job by that of a random sample of 50 such women will be at most 20 weeks
Suppose there is a city where the mean cost per month of a one-bedroom apartment is $1,500, with a standard deviation of $250. Approximately what percentage of one-bedroom apartments in the city cost between $750 and $1,000?
A successful basketball player has a height of 6 feet 11 inches, or 211 cm. Based on statistics from a data set, his height converts to the z score of 5.17. How many standard deviations is his height above the mean?
An air condition company will spend an average of 64 minutes with a standard deviation of 19 minutes on a service call. Based on this, and assuming a normal distribution, 5% of service calls will take more than how much time to complete? Approximately 66.29 minutes O Approximately 32.75 minutes O Approximately 39.41 minutes O Approximately 95.25 minutes O Approximately 77.23 minutes
In the class of 2019, more than 1.6 million students took the SAT. The distribution of scores on the math section (out of 800) is approximately normal with a mean of 528 and standard deviation of 117. What proportion of students earned scores between 500 and 600 on the SAT math test?
The president of a college wants to determine the mean number of units that college students take per semester. How large of a sample is required in order to be 99% sure that a sample mean will be off by no more than 1.25 units? An initial study suggested that the standard deviation is approximately 2.1 units.
A parenting magazine reports that the average amount of wireless data used by teenagers each month is 5 Gb. For her science fair project, Ella sets out to prove the magazine wrong. She claims that the mean among teenagers in her area is less than reported. Ella collects information from a simple random sample of 25 teenagers at her high school, and calculates a mean of 4.7 Gb per month with a standard deviation of 0.9 Gb per month. Assume that the population distribution is approximately normal. Test Ella's claim at the 0.01 level of significance. Step 3 of 3: Draw a conclusion and interpret the decision. E Tables E Keypad Answer Keyboard Shortcuts We reject the null hypothesis and conclude that there is sufficient evidence at a 0.01 level of significance that the average amount of wireless data used by teenagers each month is less than 5 Gb. We fail to reject the null hypothesis and conclude that there is insufficient evidence at a 0.01 level of significance that the average amount of…

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS