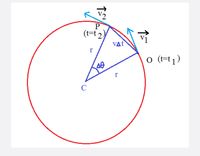
Make a drawing of the path of an object in circular motion at constant speed. On that path, use a dot to represe the object's position at time t1. Label this point as O, and draw a vector at O to represent the magnitude and direction of the object's velocity at time t. Draw another dot to represent the object's position at a later time t2 shortly after t1, and label this point P. Drawa vector at P to show the magnitude and direction of the object's velocity at time t2. 2. Redraw the velocity vectors with the tail of one vector (point P) at the tail of the other vector (point O). Keep the same size and direction as in the previous drawing. To find the acceleration of the object, you are interested change in velocity (Av). The change Av is the increment that must be added to the velocity at time t so that the resultant velocity has the new direction after the elapsed time At = tj – t2. Add the change in velocity Av to you the drawing of the velocity vectors; it should be a straight line connecting the heads of the vectors. 3. On your drawing from question 1, label the distance r from the center of the circle to points O and P. In the limit that the time interval is very small, the arc length distance traveled by the object can be approximated as a straight line. Use this approximation to label the distance traveled by the object along the circle from point O to P in terms of the object's velocity and the elapsed time. 4. The triangle drawn in question 2 (with v and Av) is similar to the triangle drawn in question 3 (with r and the straight line distance traveled by the object) because they have the same apex angle. Use the relationship of similar triangles to write an equation that connects the sides and the bases of the two triangles. 5. Solve your equation for Av/At to get an expression for the acceleration in terms of the object's uniform velocity and the distance r. 6. From your equation, is the acceleration of an object in circular motion ever zero? Does the magnitude of the acceleration change with time?

Calculate the image distance when an object is placed 6 cm in front of a mirror with focal length -10 cm.(Give your answer in centimeters but don't include units in your answer.)

A concave mirror of focal length 17.5 cm forms a real image 24.8 cm from the mirror. What is the magnification? (Mind your minus signs.) (Unit = cm)

Consider the compound optical system shown in the diagram, where two thin lenses of focal lengths 7.5 cm (left lens) and 35 cm (right lens) are separated by a distance 25 cm.     If a 2.9 cm tall object is placed as indicated in part (a), and the image formed is 0.74 cm tall, what is the magnification of the first lens?  M1 =  b. Using the information from part (a), calculate the image distance, in centimeters, from the first lens.  di1 =