Let $ X_1 $ and $ X_2 $ be independent exponential distributions with the same parameter $ \lambda $. What is the joint distribution of $ Y_1 = X_1 + X_2 $ and $ Y_2 = \frac{X_1}{X_1 + X_2} $? What are the distributions of $ Y_1 $ and $ Y_2 $?

Given: X1 & X2 are independent random variables with pdfs f(x1)=λe-λx1; x1>0…

Answered: Let X, and X, be independent…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Question

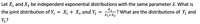
Let $ X_1 $ and $ X_2 $ be independent exponential distributions with the same parameter $ \lambda $. What is the joint distribution of $ Y_1 = X_1 + X_2 $ and $ Y_2 = \frac{X_1}{X_1 + X_2} $? What are the distributions of $ Y_1 $ and $ Y_2 $?

Expert Solution

Step 1

Given: X₁ & X₂ are independent random variables with pdfs

$f (x_{1}) = λ e^{- λ x_{1}}; x_{1} > 0$ & $f (x_{2}) = λ e^{- λ x_{2}}; x_{2} > 0$

Then their joint pdf f(x₁, x₂) (say) is given by

$f (x_{1}, x_{2}) = f (x_{1}) f (x_{2}) = λ^{2} e^{- λ (x_{1} + x_{2})}$

We are given

$Y_{1} = X_{1} + X_{2} & Y_{2} = \frac{X_{1}}{X_{1} + X_{2}}$

First, we find the joint density of $Y_{1} & Y_{2}$

Let $T (x_{1}, x_{2}) = (x_{1} + x_{2}, \frac{x_{1}}{x_{1} + x_{2}})$ , then T is a bijection from $[0, \infty) \times [0, \infty) o n t o [0, \infty) \times [0, 1]$ . Now we need to find $(x_{1}, x_{2})$ in terms of $(y_{1}, y_{2})$ .

Multiplying Y₁ & Y₂ we get

$x_{1} = y_{1} y_{2}$ then $x_{2} = y_{1} - x_{1} = y_{1} - y_{1} y_{2}$

So, $T^{- 1} (y_{1}, y_{2}) = (y_{1} y_{2}, y_{1} - y_{1} y_{2})$

The Jacobian of transformation is

$J = \frac{δ (x_{1}, x_{2})}{δ y_{1} δ y_{2}} = |\begin{matrix} \frac{δ x_{1}}{δ y_{1}} & \frac{δ x_{2}}{δ y_{1}} \\ \frac{δ x_{1}}{δ y_{2}} & \frac{δ x_{2}}{δ y_{2}} \end{matrix}| = |\begin{matrix} y_{2} & 1 - y_{2} \\ y_{1} & - y_{1} \end{matrix}| = - y_{1}$

Thus the joint pdf of Y₁ and Y₂, g(y_1,y₂) is

$g (y_{1}, y_{2}) = f_{X_{1} X_{2}} (x_{1}, x_{2}) \times | J | = f_{X_{1}} (x_{1}) f_{X_{2}} (x_{2}) \times y_{1} = f_{X_{1}} (y_{1} y_{2}) f_{X_{2}} (y_{1} - y_{1} y_{2}) y_{1} = λ e^{- λ y_{1} y_{2}} \cdot λ e^{- λ (y_{1} - y_{1} y_{2})} y_{1} = λ^{2} y_{1} e^{- λ y_{1}} ∴ g (y_{1}, y_{2}) = \{\begin{cases} λ^{2} y_{1} e^{- λ y_{1}}; y_{1} \geq 0, 0 \leq y_{2} \leq 1 \\ 0; o t h e r w i s e \end{cases}$

Therefore, the marginal pdf of Y₁ is

$g (y_{1}) = \int_{0}^{1} g (y_{1}, y_{2}) d y_{2} = \int_{0}^{1} λ^{2} y_{1} e^{- λ y_{1}} d y_{2} = λ^{2} y_{1} e^{- λ y_{1}} {|y_{2}|}_{0}^{1} = λ^{2} y_{1} e^{- λ y_{1}} ∴ g (y_{1}) = \{\begin{cases} λ^{2} y_{1} e^{- λ y_{1}}; y_{1} \geq 0 \\ 0; o t h e r w i s e \end{cases}$

Step by step

Solved in 2 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Multivariate Distributions and Functions of Random Variables$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions