Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Suppose A is a 2 by 3 matrix. Does Ax = 0 always have infinitely many solutions? Give a reason. Does…
A:
Q: 4: Let H1 and H2 be two subspaces of R". Show that H1 n H2 is also a subspace of R".
A: To show a set W to be a subspace of the of a space X if a,b∈W then a+b∈W   and for a scaler λ and…
Q: Give an example of a subset (not subspace) of R3 that has an infinite number of elements, is closed…
A: A subset W of vector space V over the scalar field K is a subspace of V if and only if following…
Q: Let S be a subspace of R" and let S be its orthogonal complement. Prove that S- is also a subspace…
A:
Q: 2. Let P3(R) be the vector space of all polynomials of degree 3 or less (and the zero polynomial).…
A:
Q: Determine the dimension of the vector space given by -a V = | a,b E R a b
A: Given V = -aa0, -b0b | a, b ∈ℝ
Q: Determine if all polynomials P = ao + a,x + a,x² + a3x³ , with ao, a1, a2, az integer, is subspace…
A:
Q: be the vector space of all polynomials of degree 3 or less in the variable z. Let PI(T) 2+x+1²,…
A: In this question, we check the given set forms a basis or not. Then we use elementary transformation…
Q: 19. Prove that the set of all vectors in R³that satisfy the equation x₁ = 3x2, is a subspace.
A: (.)  Let set  'S'  is given by ,        S=x1,x2,x3∈ℝ3  :  x1=3x2 or   S= x1,x2,x3∈ℝ3 :  x1-3x2=0…
Q: Let S be the set of all ordered pairs of real numbers (x1, x2) equipped with the following…
A:
Q: Let Rz, be a linear space with all polynomials p(x)= ar² + bx+c(a,b,c R) whose degree is no more…
A: Note: As per our guidelines, we can answer the first question. Please repost the remaining…
Q: Use the function to find the image of v and the preimage of w. T(V1, V2, V3) = (V2 - V, V1 + V2,…
A:
Q: Determine whether or not W = {[a, a?, b] | a and b are real numbers} is a subspace of R³. Justify…
A: See the detailed solution below.
Q: Find scalars x, y and z such that x(2, 1, 4) + y(1,−1, 3) + z(3, 2, 5) = (6,11,6)
A:
Q: Create a matrix B that fits within the scope of Hermitian Matrices, write, and solve a linear…
A: Consider the matrix B with complex entries ( over C), then the conjugate transpose of B is defined…
Q: Which of the following sets are subspaces of R³: W1 = {(x1, x2, X3) : x3 = 2x1 – 4x2}; W2 = {(x1,X2,…
A:
Q: Let P, is the vector space of polynomials of the degrees2.Use coordinate vectors to that the…
A: The main objective is to check {p1,p2,p3} linear independent and basis of P2.
Q: Are all functions from one vector space to another linear?
A: Let f: V→W is a  map from vector  V to W such that fx=x2 The given example the function from one…
Question
Let \( M \) be the set of all vectors (or polynomials) \( x \) in \( \mathscr{P} \) (over \( \mathbb{R} \)) for which \( x(t) = x(-t) \)—even polynomial functions—holds identically in \( t \). Show that \( M \) is a subspace of \( \mathscr{P} \) (over \( \mathbb{R} \)).
expand button
Transcribed Image Text:Let \( M \) be the set of all vectors (or polynomials) \( x \) in \( \mathscr{P} \) (over \( \mathbb{R} \)) for which \( x(t) = x(-t) \)—even polynomial functions—holds identically in \( t \). Show that \( M \) is a subspace of \( \mathscr{P} \) (over \( \mathbb{R} \)).
Expert Solution
Check Mark
Subspace test:

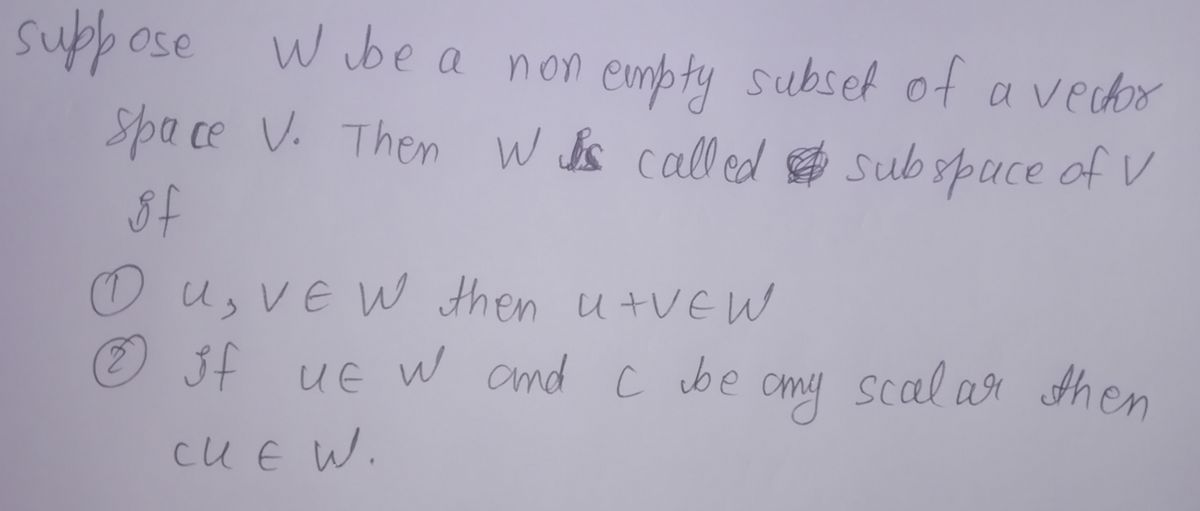
Advanced Math homework question answer, step 1, image 1

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS