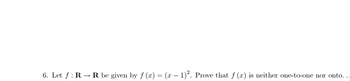
Let f: R → R be given by f (x) = (x − 1)². Prove that f(x) is neither one-to-one nor onto.

4. Consider the formula A = Vx (p(x) →q(x)) → (Vxp(x) →xq(x)). (a) Show that A is valid. (b) Show that the converse of A is not valid.

We have learned the mid-point and trapezoidal rule for numercial intergration in the tutorials. Now you are asked to implement the Simpson rule, where we approximate the integration of a non-linear curve using piecewise quadratic functions. Assume f(x) is continuous over [a, b] . Let [a, b] be divided into N subintervals, each of length Ax, with endpoints at P = x0, x1, x2,.. Xn,..., XN. Each interval is Ax = (b − a)/N. The equation for the Simpson numerical integration rule is derived as: f f(x) dx N-1 Ax [ƒ(x0) + 4 (Σ1,n odd f(xn)) ƒ(x₂)) + f(xx)]. N-2 + 2 (n=2,n even Now complete the Python function InterageSimpson (N, a, b) below to implement this Simpson rule using the above equation. The function to be intergrate is ƒ(x) = 2x³ (Already defined in the function, no need to change).

For f (a, b) = (a | b) | b(a) Simplify f (a, b).(b) Find DNF for f (a, b).(c) Is f (a, b) satisfiable?