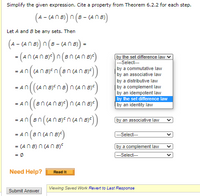
How to enter the proper answer Simplify the given expression. Cite a property from Theorem 6.2.2 for each step.(A - (AN B) n (8 - (A n B)Let A and 8 be any sets. Then(A - (AN B) n (B -- (A N B) =- (ancana) n(3ncanBy)by the set difference law v--Select---by a commutative lawby an associative lawby a distributive lawby a complement lawby an idempotent lawby the set difference lawby an identity law- An((An B)E n (8n (An B))= An(((AN B)an(sncano)ncan)= An((Br= An(Bn((AN B)en (AN B)<)by an associative law- An (an (An By)= (AN B) n (AN B)°= Ø---Select--by a complement law|---Select--Need Help?Read ItViewing Saved Work Revert to Last ResponseSubmit Answer

Answered: Image /qna-images/answer/9fe552cf-2883-4269-a30e-a29be08a79cc.jpg

Let A and 8 be any sets. Then (A - (A N B) n (8 - (An5) - - (4ก (A ก อ) ก (8n (An ๒) - an(anosn(ancana) an(canorna)ncans) -an(ancanor)ncano) - an(sn(anasncano) -an(ancanay) by the set difference law ---Select--- by a commutative law by an associative law by a distributive law by a complement lavw by an idempotent law by the set difference law by an identity law by an associative law -Select-- = (AN B) N (A N B) by a complement law -Select--

Let A and 8 be any sets. Then (A - (A N B) n (8 - (An5) - - (4ก (A ก อ) ก (8n (An ๒) - an(anosn(ancana) an(canorna)ncans) -an(ancanor)ncano) - an(sn(anasncano) -an(ancanay) by the set difference law ---Select--- by a commutative law by an associative law by a distributive law by a complement lavw by an idempotent law by the set difference law by an identity law by an associative law -Select-- = (AN B) N (A N B) by a complement law -Select--

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

select all the expressions that are equivalent to 8/12 choice answers: 8 times 1/12 2 times 4/12 4 times 4/12 4 times 2 times 1/12 12 times 1/8 please tell me the ones to select
A realtor uses a lockbox to store the keys to a house that is for sale. The access code for the lock box consists of four digits. The first digit cannot be zero and the last digit must be off. How many different codes are available
How many interpretations are there for the number 5000? Express your answer as an integer.
What are the correct answers ?
Use the multiplication principle to solve the problem.How many different 7-digit phone numbers are possible if the first digit cannot be a 0?
Solve step by step in digital formatXXXXXXXXXXXXXXXXXXXXX3. How many different five-digit numbers can be formed using only the digits of the number 75, 226, 522? Hint: consider numbers with one 2 first, then two 2, etc.
But why is it that the answer in the answer key is C? How to get the answer using the calculator? Thanks!
Users of the online system for a Bank are required to set a password that is 10 character-long. Each character can be a letter, a 1-digit number, or a symbol from the list: !, @, #, &, % How many passwords are possible if there is no distinction between upper case and lower case letters? (Not Case-sensitive) How many passwords are possible if the first and last digits have to be numbers?
1: Find all the number for which the expression is not defined
How did you get the values in the able?
I need help with 1-38
How many different words consisting of 7 letters can be written using the letters {A A A B C N K}?