The complex numbers Z₁ and Z₂ are defined as follows:4₁ = 6 (cos(4) + i sin(²sin(4))Z₂ = 12 (cos(T) + i sin())Calculate|Z| =0 =O-3TT/5a =in polar form, where Z = |Z| (cos(0) + i sin(0))Z₂b=03π/3O-π/504TT/5ОпCalculate Z in rectangular form, where Z = a + b i: Write your answers to 2 deciplacesОπ/2

The given complex numbers are…

The complex numbers Z₁ and Z₂ are defined as follows: ²1 6 (cos(4) + i sin(4T)) = Z₂ Calculate = 12 (cos(T) + i sin()) |Z| = 8 = O-3π/5 a = b= ²₁ in polar form, where Z= |Z| (cos(0) + i sin(0)) ²₂ 03π/3 O-TT/5 04T/5 Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 de places OTT Оπ/2

The complex numbers Z₁ and Z₂ are defined as follows: ²1 6 (cos(4) + i sin(4T)) = Z₂ Calculate = 12 (cos(T) + i sin()) |Z| = 8 = O-3π/5 a = b= ²₁ in polar form, where Z= |Z| (cos(0) + i sin(0)) ²₂ 03π/3 O-TT/5 04T/5 Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 de places OTT Оπ/2

Algebra & Trigonometry with Analytic Geometry

13th Edition

ISBN:9781133382119

Author:Swokowski

Publisher:Swokowski

Chapter11: Topics From Analytic Geometry

Section: Chapter Questions

Problem 34RE

See similar textbooks

Related questions

Q: 2. If z = cos 0 + i sin 0 where 0 is real, show that 1 1 - i tan- = - 1+z 2z 1-z2 Express: а) 1+z2…

Q: b) 6(sin x)² + cos 2x + 1 = 0 [0,2π] I

A: Solution6 sin2x+cos 2x+1=0we know cos 2 x= 1-2 sin2xput this value in the given equation,6 sin2 x+…

Q: We have shown that in the case of complex conjugate roots,r =a±ib,b̸=0, of the indicial equation,…

A: The solution of some differential equation: Actually our task is to express the term in bracket…

Q: Let z = 7 (cos (7π/9) + i sin (7π/9)) and w = 6 (cos (2π/3) + i sin (2π/3)). If zw is expressed…

A: Introduction: A complex number has many different representations. These are the rectangular…

Q: Find the produCtI' 22 n polar form, Wnerezi and 2 are BIVEN below. 21 = 4(cos(61"+i sin(61") 22 = 5…

A: According to Euler's identity, r ( cos x + i sin x) = r eix

Q: The complex numbers Z₁ and Z₂ are defined as follows: ²₁ = 5 (cos(²) + i sin(2)) ²₂ = = 2 (cos() + i…

Q: 2. By hand, sketch the following against independent variable t: a) x₁(t) = Re(2e(-1+j2m)t) b) x₂(t)…

Q: Put in polar form z -3(cos(6) + i sin(6)). What is its principle argument, Arg(z)?

Q: O For y = Asin (x- C)] + D Identify with graph A. B, C and D for the sin function y = -2sin (;x -) +…

Q: Prove that, 2cos 2"0 +1 (2 cos 0 – 1)(2 cos 20 – 1)(2cos 2²e – 1...(2cos 2"–19 – 1) 2 cos 0+1

A: Let us take theta=a. So replacing theta with a, We'll multiply both sides by 2cosA + 1 and we'll…

Q: 12) Based on below complex functions, what is W¹? W₂ 30y - 8 (Cos (4) + + sin (47)) 3 103 = 2 (cos…

A: we have given that w1=8cos4π3+isin4π3w2=2cos7π3+isin7π3 then what is w1w=?

Q: Find the solution. (D4+2D³ + 10D²)y =0. y = c,+c,x+e¯*(c,cos3x +c,sin3x) C B y = (c,+c,)x+e-(c,cos3x…

A: Given Differential equation is D2+2D3+10D2y = 0

Q: a) Express z = e(4+i(37/4)) in Cartesian form. b) Express z = cos(3i)+In(-3– 3i) in Cartesian form.

Q: 7. Find the rectangular equation if r = 4 cos 0 + 4 sin 0 (a) (c) x² + y² = 4 x² + y² = 4(x + y) (b)…

Q: The complex numbers ₁ and ₂ are defined as follows: 21 = 3(cos()+isin()) 22 = 5(cos()+isin()…

Q: (d) Let Z₁ = −4+ 8i and Z₂ = -1 -2i. Show that (i) 21/2₂ | = 4. | (ii) (iii) |z₁|² +Z₁ Z₂ = 100.…

Q: Find all non - zero complex numbers z satisfying z =i z.

Q: 1 Let f (z) z - 8 Part (a) Integrate the function f (z)along the curve C the complex plane given by…

A: Using the Cauchy integral theorem on the closed contour for part(b).

Q: w=tan inverse[ ((1-z)/(1+z)) ] is a complex function, what is the mapping conformal of unit circle…

A: We will find the first seethe image of (1-z)/(1+z) when IzI=1

Q: The complex numbers ₁ and ₂ are defined as follows: 2₁ = 3(cos() + isin()) 22 =2(cos(¹)+isin()…

Q: O Find all periodic solutions of the equation y" - 3y + 2y = sin.x.

Q: The function f (x) = 10 + 2 cos(14x) + cos(11x) + 2 sin(7x) − cos(4x) + 5 cos(3x) is called The…

A: Solution: To find the length ∣∣f(x)∣∣ of the Fairy Godmother curve…

Q: (a) Given w = √3-i, (i) express w in polar form. (ii) find all the roots of 25 = √3-i in polar form.…

Q: . Show all pertinent solutions. 8. y = arc sin(-) 9. y = arccos 0 10. y = tan'' (-1)

Q: 4) Let z= 1+ V 3 i. Compute all values of z". Exponential notation is sufficient. Sketch these…

A: Given: z=1+3i

Q: b) 2 cos² x + 3 cosx+1 = 0

A: Step 1: Step 2: Step 3: Step 4:

Q: y" - 2y y""y" + 2y = e2 (cosx-3 sin r). 21 - 4y + 4y = 5-e + c²r.

Q: 3. Express the following complex numbers in polar form( r< θ), find the modulus ‘r’ and argument θ”…

Q: Let z = 9(cos 2.3+isin 2.3). Write the following numbers in the polar form r(cos o + i sin ø), 0 < o…

A: Here, the given complex number is: z=9(cos 2.3+ sin 2.3) Comparing the number z with r(cos ϕ+i sin…

Q: a) 2(sin x)² - 1 = 0 [0,2π]

A: a) 2(sin⁡x)2−1=0[0,2π]

Question

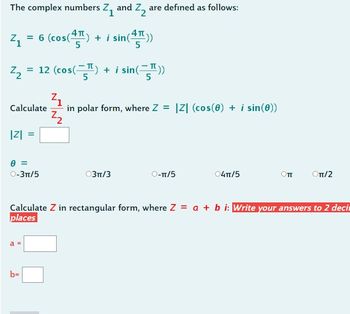
The complex numbers Z₁ and Z₂ are defined as follows:
4₁ = 6 (cos(4) + i sin(²
sin(4))
Z₂ = 12 (cos(T) + i sin())
Calculate
|Z| =
0 =
O-3TT/5
a =
in polar form, where Z = |Z| (cos(0) + i sin(0))
Z₂
b=
03π/3
O-π/5
04TT/5
Оп
Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 deci
places
Оπ/2

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1: Given Information

VIEW

Step 2: Calculation for part 1

VIEW

Step 3: Calculation for part 2

VIEW

Solution

VIEW

Step by step

Solved in 4 steps with 27 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

how did you came up with pi

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions

The complex numbers Z₁ and Z₂ are defined as follows: ²1 i sin (2T)) ²₂ = 3 (cos(8) + i sin(8)) ²1 in polar form, where Z = IZ] (cos(0) + i sin(0)) 2₂ = Calculate |Z| = 0 = O-2π/3 a = + 9 (cos(2) b= 02π/3 OTT/3 O-π/3 08 Calculate Z in rectangular form, where Z= a + b i: Write your answers to 2 decin places O-TI
The complex numbers Z₁ and Z₂ are defined as follows: = 4 (cos(²T) + i sin(²) ²₁ Z₂ Calculate = 8 (cos() |ZI = 0 = O-2π/3 a = b= + i sin()) ²1 in polar form, where Z = |Z] (cos(0) + i sin (0)) ²₂ 02π/3 Oπ/3 O-TT/3 Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 decimal places O-TT
The complex numbers Z₁ and Z₂ are defined as follows: Z₁ = 3 (cos(−2¹) + i sin(−2π)) 4 4 ²₂ = 2 (cos(³) + i i sin (³1)) 4 4 Calculate Z₁ x Z₂ in polar form, where Z = IZ] (cos(0) + i sin (0)) |ZI = 8 = -3TT/4 a = 03TT/4 b= 00 OTT/4 O-TT/4 аз Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 decimal places ОTT/2
The complex numbers Z₁ and Z₂ are defined as follows: 7₁ = 5 (cos(²) + i sin(²)) Z₂ = 2 (cos() + i sin()) Calculate Z₁ x Z₂ in polar form, where Z = |Z| = 0 = O-2π/6 a = 02π/6 b= |Z] (cos(0) + i sin (0)) Оπ/6 O-TT аз Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 decimal places Оп
The complex numbers ₁ and ₂ are defined as follows: 2₁ = 5(cos(-) + isin(-)) 2₂=2(cos(¹)+isin (3) Calculate z₁ X 22 |2| 0 = O-T/2 a in polar form, where z = |z|(cos(0)+isin (0)) Calculate z in rectangular form, where z = a + bi b Ont/4 03π/4 On/2 Оп O-T
3. Express the following complex numbers in polar form( r< θ), find the modulus ‘r’ and argument θ” and also represent the results on the Argand diagram.(a) z1=3+ 4j(b) z2= -3+4j(c) z3= z2-z1
Find z1z2 in polar form. z1 = 5(cos(170)+i sin(170)) : z2 = (1/2) (cos(10)+i sin(10)
The complex number Z is defined as follows: z = (-1+√3 i)4 Calculate Z in polar form, where Z = |Z| (cos(0) + i sin (0) ) Enter solution including 2 decimal places. Example if Z = 2 enter 2.00 Z= = ОTT/2 Check 00 Оп O-π/2 ○2π/3 O-2π/3
The complex numbers Z₁ and Z₂ are defined as follows: = 0.5 (cos(-2) + i sin(-2)) 6 6 ²1 ²₂ Calculate Z₁ x Z₂ in polar form, where Z = |Z| (cos(0) + i sin (0)) |Z| = = 4 (cos(ST) + i sin(ST)) 0 = O-2π/3 a = b= 02π/3 Оπ/6 O-π/6 Calculate Z in rectangular form, where Z = a + b i: Write your answers to 2 decimal places OTT/2 O-TT/2