
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
can someone help me solve for x and y ? on #4
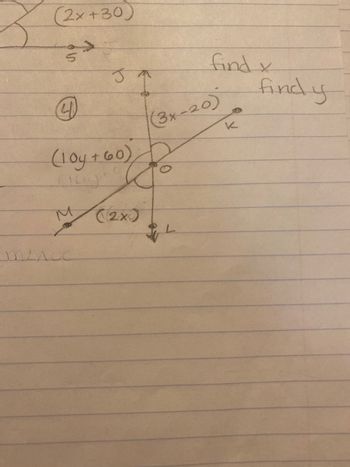
Transcribed Image Text:### Diagram and Equations Illustrating Angle Relationships
This image is a hand-drawn diagram showcasing several geometric relationships and equations involving angles formed by intersecting lines. The primary objective posed by the image is to **find the values of \(x\) and \(y\)**.
#### Description of Diagram
- **Lines and Angles**:
- The diagram displays three lines intersecting at the point labeled \(O\).
- The angles at point \(O\) have the following expressions:
- Angle MOJ is expressed as \((10y + 60)^\circ\).
- Angle KOL is expressed as \((2x)^\circ\).
- Angle JOK is expressed as \((3x - 20)^\circ\).
- **Labels**:
- The points where the lines intersect with the circle around \(O\) are labeled \(J\), \(K\), \(L\), and \(M\).
The problem asks to **find the values of the variables \(x\) and \(y\)**.
### Solving the Problem
Given that the lines form angles around point \(O\), we can use the fact that the sum of angles around a point is 360 degrees to write the following equation:
1. \((10y + 60) + (3x - 20) + (2x) = 360\)
2. Simplifying this, we get:
- Combine like terms: \(10y + 3x - 20 + 2x = 360\)
- Further simplifying: \(10y + 5x - 20 = 360\)
- Add 20 to both sides: \(10y + 5x = 380\)
- Dividing everything by 5: \(2y + x = 76\)
This gives a linear equation relating \(x\) and \(y\). To find unique values for \(x\) and \(y\), we would need one more independent equation, involving either \(x\) or \(y\). The image does not provide further information to derive a second equation directly.
However, assuming additional contextual information or conditions provided in class or problem set might be necessary to solve for unique values of \(x\) and \(y\). In the absence of additional constraints, you would solve the above equation based on the additional condition or using substitution if any
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning