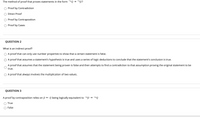
The method of proof that proves statements in the form 79 →p?Proof by ContradictionDirect ProofProof by ContrapositionProof by CasesQUESTION 2What is an indirect proof?A proof that can only use number properties to show that a certain statement is false.O A proof that assumes a statement's hypothesis is true and uses a series of logic deductions to conclude that the statement's conclusion is true.A proof that assumes that the statement being proven is false and then attempts to find a contradiction to that assumption proving the original statement to betrue.A proof that always involves the multiplication of two values.QUESTION 3A proof by contraposition relies on p + q being logically equivalent to p → 79TrueFalse The method of proof that proves statements in the form p → q?Direct ProofProof by CasesProof by ContrapositionO Proof by ContradictionQUESTION 5To prove the following statement using a proof by contradiction, what assumption would the proof start with?Statement: There is an infinite number of prime numbers.There are no prime number less than 100There is a finite number of prime numbersThere is an infinite number of prime numbersThere are no even prime numbersQUESTION 6If we wanted to prove the following statement using a proof by contradiction, what assumption would we start our proof with?Statement: When x and y are odd integers, there does not exist an odd integer z such that x + y = z.When x and y are odd integers, there does not exist an even integer z such that x + y = z.When x and y are odd integers, there does exist an odd integer z such that x + y = z.

Name: The method of proof that proves statements in the form 79 →p?Proof by
Uploaded: 2024-03-20T06:38:44.000Z
Channel: Bartleby
Description: The method of proof that proves statements in the form 79 →p?Proof by ContradictionDirect ProofProof by ContrapositionProof by CasesQUESTION 2What is an indirect proof?A proof that can only use number properties to show that a certain statement is f

Answered: Image /qna-images/answer/376010f0-68dd-48d4-a0cf-dfb77b4798e4.jpg

Answered: indirect proof? of that can only use…

Math

Advanced Math

indirect proof? of that can only use num

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

3. (Р5, Раge 16; Prove that a <0. (You may have to use Proof by Contradiction and Archimedean Property, Part ii.) Suppose that the number a has the property that for every natural number n, a < 1/n.
pls, help me. thank you so much!
Mathmatics 1. Prove that for all positive natural numbers n,13 + 23 + ... + n3 = n2⋅(n+1)2/4
Prove with details the following statement:Top statement is the question and bottom statement is the answer.
13-4i|.|3+4jl= ... 20 5 -5 25 оооо
not use ai please