
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
In the following question:
" Let a, b ∈ Z. Show that if a ≡ 5 (mod 6) and b ≡ 3 (mod 4), then 4a + 6b ≡ 6 (mod 8)."
why do we ignore the -6 when substituting the variables of a and b, if we expand "4a + 6b ≡ 6 (mod 8)" we get (4a+6b)-6=8y, when we substitute we have to end up with the 8y right? Im just confused why the -6 is ignored?
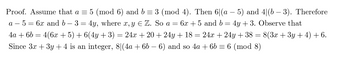
Transcribed Image Text:Proof. Assume that a = 5 (mod 6) and b = 3 (mod 4). Then 6|(a - 5) and 4|(b − 3). Therefore
a 5= 6x and b- 3 = 4y, where x, y E Z. So a = 6x +5 and b = 4y + 3. Observe that
4a + 6b = 4(6x + 5) + 6(4y + 3) = 24x +20 +24y + 18 = 24x + 24y + 38 = 8(3x + 3y + 4) + 6.
Since 3x + 3y + 4 is an integer, 8|(4a + 6b − 6) and so 4a + 6b = 6 (mod 8)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- 2. Solve the simultaneous congruences x = 4 (mod 5) and 2x = 3 (mod 7)arrow_forwardDoes x2 + 5x congruent to 12 (mod 31) have a solution? (Hint: complete the square)arrow_forwardTrue or false: If a and b are integers satisfying 4a congruent 4b(mod 20), then a congruent b (mod 5). Justify your answerarrow_forward
- I need detailed step by step answer. Also please don't copy the answer from other online sitesarrow_forwardSolve the following equations in Z, giving full details of your analysis: (a) 5x + 3 = 1 (mod 6) (b) 6x-5 = 5 (mod 6) (c) 50x63 (mod 71)arrow_forward4. Determines the result of the following operations: a. (27 – 3) (mod 5) b. (56 – 14) (mod 7) c. (6+7) (mod 2)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

