Prove this claim: Do not copy For every positive integer d and every integer n, the following equation is satisfied: (n² ) div d = (d)( n div d)² + ( 2 )( n div d)( n mod d) + (((n mod d)²) div d) for distri ● + Strategy: Begin your proof by supposing that d is a positive integer and n is an integer (and do not assume anything more). Based on that limited information you must establish the correctness of the asserted equation. ● ● RUG DU ● You can assume that the reader accepts the truth of the Quotient-Remainder Theorem, but they might not remember the definitions of the "div" and "mod" operators associated with integer division; reminders are in order. Take care of that before launching into the gory details of your argument. State that the (ordinary) Quotient-Remainder Theorem justifies these statements concerning the existence and et couniqueness of certain quotients and remainders obtained through integer division using the divisor d: ● copy-Not (1) 31 (9₁, ₁) = ZxZ, (n = dq₁ + ₁)^(0 ≤r₁
Prove this claim: Do not copy For every positive integer d and every integer n, the following equation is satisfied: (n² ) div d = (d)( n div d)² + ( 2 )( n div d)( n mod d) + (((n mod d)²) div d) for distri ● + Strategy: Begin your proof by supposing that d is a positive integer and n is an integer (and do not assume anything more). Based on that limited information you must establish the correctness of the asserted equation. ● ● RUG DU ● You can assume that the reader accepts the truth of the Quotient-Remainder Theorem, but they might not remember the definitions of the "div" and "mod" operators associated with integer division; reminders are in order. Take care of that before launching into the gory details of your argument. State that the (ordinary) Quotient-Remainder Theorem justifies these statements concerning the existence and et couniqueness of certain quotients and remainders obtained through integer division using the divisor d: ● copy-Not (1) 31 (9₁, ₁) = ZxZ, (n = dq₁ + ₁)^(0 ≤r₁
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please don't send me the previous posted answer of this question
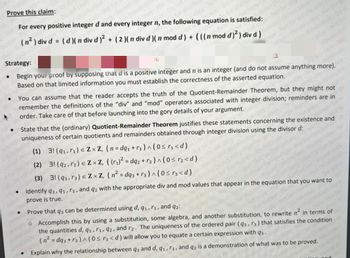
Transcribed Image Text:Prove this claim:
Do not copy
For every positive integer d and every integer n, the following equation is satisfied:
(n² ) div d = (d)( n div d)² + ( 2 )( n div d)( n mod d) + (((n mod d)²) div d)
for distru
●
Strategy:
re
Begin your proof by supposing that d is a positive integer and n is an integer (and do not assume anything more).
Based on that limited information you must establish the correctness of the asserted equation.
●
+
●
copy No
You can assume that the reader accepts the truth of the Quotient-Remainder Theorem, but they might not
remember the definitions of the "div" and "mod" operators associated with integer division; reminders are in
order. Take care of that before launching into the gory details of your argument.
State that the (ordinary) Quotient-Remainder Theorem justifies these statements concerning the existence and
et couf uniqueness of certain quotients and remainders obtained through integer division using the divisor d:
ution-Do
ions Do
●
●
copy-Not
distribution
(1) 31 (9₁, ₁) = ZxZ, (n=dq₁ + ₁)^(0 ≤r₁ <d)
(2) 3! (92,7₂) € ZXZ, ((r₁)² = dq2 + r₂)^(0 ≤ r₂<d)
(3) 31 (93,73) € ZXZ, (n² = dq3 +r3) ^ (0≤r³<d)
Identify 93, 91, r₁, and q2 with the appropriate div and mod values that appear in the equation that you want to
prove is true.
NOT BASE
wwwms Do
et or
Prove that q3 can be determined using d, q1, r1, and 92:
o Accomplish this by using a substitution, some algebra, and another substitution, to rewrite n² in terms of
the quantities d, q1, r1, 92, and r2. The uniqueness of the ordered pair (93, r3) that satisfies the condition
(n² = dq3+13)^(0 ≤ 3<d) will allow you to equate a certain expression with q3.
Explain why the relationship between q3 and d, 91, r₁, and q2 is a demonstration of what was to be proved.
Do not co
Ma
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
