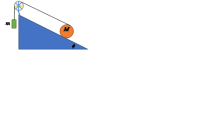
In the diagram below the solid disc (M, r) is rolling on an incline and the pulley is ideal. Find the acceleration of the block (m) and the acceleration of the CM of the disc. Analyze the possibilities of the disc to roll down vs. up the incline.

A thin, light string is wrapped around the rim of a 4.10 kg, solid, uniform disk (similar to a puck on ice without friction) that is 26.5 cm in diameter. A person pulls (to the right direction) on the string with a constant force of 102.0 N tangent to the disk. The disk is not attached to anything and is free to move and turn. 1) Find the angular acceleration of the disk about its center of mass. Express your answer in radians per second squared.   2) Find the linear acceleration of its center of mass. Express your answer in meters per second squared.   3) If the disk is replaced by a hollow, thin-walled cylinder of the same mass and diameter, what will be the angular acceleration of the disk about its center of mass? Express your answer in radians per second squared.   4) If the disk is replaced by a hollow, thin-walled cylinder of the same mass and diameter, what will be the linear acceleration of its center of mass? Express your answer in meters per second squared.

Solution for this problem, please. It involves the use of torque and angular acceleration.

A 3 kilogram solid sphere with a radius of 15 centimeters rolls without slipping down a rough incline with a 35 degree angle. If the sphere rolls from rest from a height of 45 centimeters, determine the sphere's translational speed at the bottom of the incline. Also, draw the free body diagram. Also see the attached picture that goes with the problem. Thank you.