
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Subject:calculas
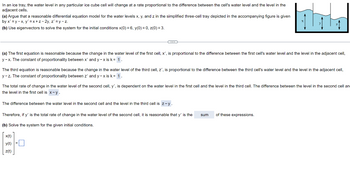
Transcribed Image Text:In an ice tray, the water level in any particular ice cube cell will change at a rate proportional to the difference between the cell's water level and the level in the
adjacent cells.
(a) Argue that a reasonable differential equation model for the water levels x, y, and z in the simplified three-cell tray depicted in the accompanying figure is given
by x'=y-x, y'=x+z-2y, z' =y-z.
(b) Use eigenvectors to solve the system for the initial conditions x(0) = 6, y(0) = 0, z(0) = 3.
(a) The first equation is reasonable because the change in the water level of the first cell, x', is proportional to the difference between the first cell's water level and the level in the adjacent cell,
y-x. The constant of proportionality between x' and y-x is k = 1.
The third equation is reasonable because the change in the water level of the third cell, z', is proportional to the difference between the third cell's water level and the level in the adjacent cell,
y-z. The constant of proportionality between z' and y-x is k = 1.
The total rate of change in the water level f the second cell, y', is dependent on the water level in the first cell and the level in the third cell. The difference between the level in the second cell and
the level in the first cell is x-y.
The difference between the water level in the second cell and the level in the third cell is z-y.
Therefore, if y' is the total rate of change in the water level of the second cell, it is reasonable that y' is the
(b) Solve the system for the given initial conditions.
x(t)
y(t) =
z(t)
sum
of these expressions.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

