MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
Imagine that before the debate, a sample of 75 likely voters had 41 who preferred candidate A. After the debate, a separate sample of 75 likely voters had 34 who preferred candidate A. Determine if the support for candidate A decreased after the debate, using alpha=0.10. By hand.
Expert Solution
arrow_forward
Step 1
Solution:
Let X1 be the number of voters who preferred candidate A before the debate, X2 bet the number of voters who preferred candidate A after the debate, n1 be the sample number of likely voters before the debate and n2 be the sample number of likely voters after the debate.
From the given information, Xl=41, n1=75, X2=34 and n2=75.
arrow_forward
Step 2
State the hypotheses.
Null hypothesis:
H0: pl–p2≤0
That is, the support for candidate A is not decreased after the debate.
Alternative hypothesis:
H1: pl–p2>0
That is, the support for candidate A is decreased after the debate.
arrow_forward
Step 3
The sample proportions are
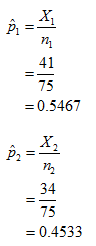
The pooled proportion is
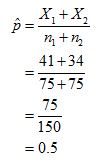
Step by stepSolved in 5 steps with 4 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- A random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.3 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.5 4.1 4.5 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Do the data indicate that the violent crime rate in the Rocky Mountain region is higher than in New England? Use ? = 0.01. Solve the problem using both the traditional method and the P-value method. (Test the difference ?1 − ?2. Round the test statistic and critical value to three decimal places.)arrow_forwardAn automobile dealer conducted a test to determine if the time in minutes needed to complete a minor engine tune-up depends on whether a computerized engine analyzer or an electronic analyzer is used. Because tune-up time varies among compact, intermediate, and full-sized cars, the three types of cars were used as blocks in the experiment. The data obtained follow. Analyzer Computerized Electronic Car Compact 51 42 Intermediate 55 43 Full-sized 62 47 Use ? = 0.05 to test for any significant differences. State the null and alternative hypotheses. H0: ?Computerized ≠ ?ElectronicHa: ?Computerized = ?ElectronicH0: ?Computerized = ?Electronic = ?Compact = ?Intermediate = ?Full-sizedHa: Not all the population means are equal. H0: ?Computerized = ?ElectronicHa: ?Computerized ≠ ?ElectronicH0: ?Compact ≠ ?Intermediate ≠ ?Full-sizedHa: ?Compact = ?Intermediate = ?Full-sizedH0: ?Compact = ?Intermediate = ?Full-sizedHa: ?Compact ≠ ?Intermediate ≠ ?Full-sized Find the value of…arrow_forwardThe table below contains data from a study of two airlines - Sunshine Airlines & Comfort Airlines - which fly from BWI to Shore City, FL. If one Airline is selected, find P (on time and Comfort Airlines). Number of Flights Arriving on Time Number of Flights Arriving Late Sunshine Airlines 33 5 Comfort Airlines 43 6arrow_forward
- Two different blood pressure medicines are being compared to determine if the average reduction in blood pressure is the same for each medication. The goal of the study is to determine if the medications differ. Twenty men age 50-60 years old are selected for the study. Ten men are chosen at random to receive the first medication and the other 10 men receive the second medication. Each of the 20 men is monitored for one month to determine the change in blood pressure over that time. Minitab provides the 95% confidence interval for (mu1 - mu2) (2.63, 14.18) a. Interpret this 95% CI. b. What assumptions (be specific) are necessary to construct this CI?arrow_forward(iii) Find (or estimate) the P-value. OP-value > 0.250 O 0.125 < P-value < 0.250 O 0.050 < P-value < 0.125 O 0.025 < P-value < 0.050 O 0.005< P-value < 0.025 OP-value < 0.005 Sketch the sampling distribution and show the area corresponding to the P-value. O -4 -2 0 2 2 M 2 DO Q -2 -2 (iv) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? Are the data statistically significant at level a? O At the a= 0.01 level, we reject the null hypothesis and conclude the data are not statistically significant. O At the a= 0.01 level, we fail to reject the null hypothesis and conclude the data are not statistically significant. O At the a= 0.01 level, we fail to reject the null hypothesis and conclude the data are statistically significant. O At the a= 0.01 level, we reject the null hypothesis and conclude the data are statistically significant. (v) Interpret your conclusion in the context of the application. O Fail to reject the null hypothesis, there…arrow_forwardDuring one month, a blood donation center found that 45.5% of the donors had the A antigen. 14.5% of the donors had the B antigen. 4.6% of the donors had the A antigen and the B antigen. 84.6% of the donors were Rh+. 87.8% of the donors had the B antigen or were Rh+. (a) Find the percent of donors that have the A antigen or the B antigen. 55.4 % (b) Find the percent of donors that have the B antigen and are Rh+. ?arrow_forward
- Bighorn sheep are beautiful wild animals found throughout the western United States. Let x be the age of a bighorn sheep (in years), and let y be the mortality rate (percent that die) for this age group. For example, x = 1, y = 14 means that 14% of the bighorn sheep between 1 and 2 years old died. A random sample of Arizona bighorn sheep gave the following information: x 1 2 3 4 5 y 15.8 17.3 14.4 19.6 20.0 Σx = 15; Σy = 87.1; Σx2 = 55; Σy2 = 1,540.45; Σxy = 272 (a) Find x, y, b, and the equation of the least-squares line. (Round your answers for x and y to two decimal places. Round your least-squares estimates to three decimal places.) x = y = b = ŷ = + x (b) Draw a scatter diagram for the data. Plot the least-squares line on your scatter diagram. (c) Find the sample correlation coefficient r and the coefficient of determination r2. (Round your answers to three decimal places.) r = r2 = What percentage of variation in y is…arrow_forwardIn 2001, the polls found that 81% of American adults believed that there was a conspiracy in the death of President Kennedy. Assume a recent poll asked 1160 American adults if they believe there was a conspiracy in the assassination and it found that 897 believe there was a conspiracy. Does the data show that the proportion of Americans who believe in this conspiracy is now lower? Test at the 9% level. What is the correct parameter symbol for this problem? What is the wording of the parameter in the context of this problem? Fill in the correct null and alternative hypotheses:arrow_forwardBighorn sheep are beautiful wild animals found throughout the western United States. Let x be the age of a bighorn sheep (in years), and let y be the mortality rate (percent that die) for this age group. For example, x = 1, y = 14 means that 14% of the bighorn sheep between 1 and 2 years old died. A random sample of Arizona bighorn sheep gave the following information: x 1 2 3 4 5 y 13.8 19.3 14.4 19.6 20.0 Σx = 15; Σy = 87.1; Σx2 = 55; Σy2 = 1554.45; Σxy = 274b) Find the equation of the least-squares line. (Round your answers to two decimal places.) ŷ = + x (c) Find r. Find the coefficient of determination r2. (Round your answers to three decimal places.) r = r2 = d) Test the claim that the population correlation coefficient is positive at the 1% level of significance. (Round your test statistic to three decimal places.) t =arrow_forward
- Bighorn sheep are beautiful wild animals found throughout the western United States. Let x be the age of a bighorn sheep (in years), and let y be the mortality rate (percent that die) for this age group. For example, x = 1, y = 14 means that 14% of the bighorn sheep between 1 and 2 years old died. A random sample of Arizona bighorn sheep gave the following information: x 1 2 3 4 5 y 15.8 17.3 14.4 19.6 20.0 Σx = 15; Σy = 87.1; Σx2 = 55; Σy2 = 1,540.45; Σxy = 272 (a) Find x, y, b, and the equation of the least-squares line. (Round your answers for x and y to two decimal places. Round your least-squares estimates to three decimal places.) x = y = b = ŷ = + xarrow_forwardDo larger universities tend to have more property crime? University crime statistics are affected by a variety of factors. The surrounding community, accessibility given to outside visitors, and many other factors influence crime rate. Let x be a variable that represents student enrollment (in thousands) on a university campus, and let y be a variable that represents the number of burglaries in a year on the university campus. A random sample of n = 8 universities in California gave the following information about enrollments and annual burglary incidents.x 12.3 28.6 24.5 14.3 7.5 27.7 16.2 20.1y 23 72 39 23 15 30 15 25 a) Compute r. (Round your answer to four decimal places.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman