
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
Fig. 8.3 included
![**Exercise 2.** Present an \(O(n)\) algorithm that sorts \(n\) positive integer numbers \(a_1, a_2, \ldots, a_n\) which are known to be bounded by \(n^2 - 1\) (so \(0 \leq a_i \leq n^2 - 1\), for every \(i = 1, \ldots, n\). Use the idea of Radix Sort (discussed in class and presented in Section 8.3 in the textbook).
Note that in order to obtain \(O(n)\) you have to do Radix Sort by writing the numbers in a suitable base. Recall that the runtime of Radix Sort is \(O(d(n+k))\), where \(d\) is the number of digits, and \(k\) is the base, so that the number of digits in the base is also \(k\). The idea is to represent each number in a base \(k\) chosen so that each number requires only 2 "digits," so \(d = 2\). Explain what is the base that you choose and how the digits of each number are calculated, in other words how you convert from base 10 to the base. Note that you cannot use the base 10 representation, because \(n^2 - 1\) (which is the largest possible value) requires \(\log_{10}(n^2 - 1)\) digits in base 10, which is obviously not constant and therefore you would not obtain an \(O(n)\)-time algorithm.
Illustrate your algorithm by showing on paper similar to Fig. 8.3, page 198 in the textbook (make sure you indicate clearly the columns) how the algorithm sorts the following sequence of 12 positive integers:
\[45, 98, 3, 82, 132, 71, 72, 143, 91, 28, 7, 45.\]
In this example \(n = 12\), because there are 12 positive numbers in the sequence bounded by 143 = \(12^2 - 1\).](https://content.bartleby.com/qna-images/question/63a2ecd4-d40e-4f58-bfeb-302941b5ae7f/54da9033-0864-4358-91a2-83f87c8e0e49/ayvygnq_thumbnail.png)
Transcribed Image Text:**Exercise 2.** Present an \(O(n)\) algorithm that sorts \(n\) positive integer numbers \(a_1, a_2, \ldots, a_n\) which are known to be bounded by \(n^2 - 1\) (so \(0 \leq a_i \leq n^2 - 1\), for every \(i = 1, \ldots, n\). Use the idea of Radix Sort (discussed in class and presented in Section 8.3 in the textbook).
Note that in order to obtain \(O(n)\) you have to do Radix Sort by writing the numbers in a suitable base. Recall that the runtime of Radix Sort is \(O(d(n+k))\), where \(d\) is the number of digits, and \(k\) is the base, so that the number of digits in the base is also \(k\). The idea is to represent each number in a base \(k\) chosen so that each number requires only 2 "digits," so \(d = 2\). Explain what is the base that you choose and how the digits of each number are calculated, in other words how you convert from base 10 to the base. Note that you cannot use the base 10 representation, because \(n^2 - 1\) (which is the largest possible value) requires \(\log_{10}(n^2 - 1)\) digits in base 10, which is obviously not constant and therefore you would not obtain an \(O(n)\)-time algorithm.
Illustrate your algorithm by showing on paper similar to Fig. 8.3, page 198 in the textbook (make sure you indicate clearly the columns) how the algorithm sorts the following sequence of 12 positive integers:
\[45, 98, 3, 82, 132, 71, 72, 143, 91, 28, 7, 45.\]
In this example \(n = 12\), because there are 12 positive numbers in the sequence bounded by 143 = \(12^2 - 1\).
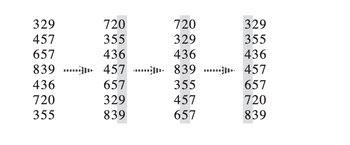
Transcribed Image Text:The image displays a series of number columns that undergo transformations through two processes. Here's a description of the process as if it were part of an educational piece explaining sorting techniques:
### Initial List:
- 329
- 457
- 657
- 839
- 436
- 720
- 355
### Step 1:
The numbers are rearranged into new columns through a sorting transformation:
- Column 1: 720, 355, 436, 457, 657, 329, 839
### Step 2:
The numbers are further rearranged:
- Column 2: 329, 436, 839, 355, 457, 657, 720
### Final Sorted List:
The final sorting arranges the numbers in ascending order:
- 329
- 355
- 436
- 457
- 657
- 720
- 839
These transformations demonstrate the steps of a sorting algorithm, showcasing how an initially unordered list of numbers is processed into a sorted sequence through successive restructuring.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- 38arrow_forwardPortrait and Landscape arearrow_forwardhe following transformations are applied to the object shown in Fig.2 1. Firstly, rotate the object ( pyramid) 90° about the z-axis, 2. Secondly, rotate the object 90° about the x-axis, 3. Thirdly, translate the object 3 units along the x-axis and 6 units along the y-axis, 4. Finally, rotate the object 90° about the y-axis axis, 5. What are the position and the orientation of the object after these transformations? Write a MATLAB Code to rotate this pyramid according to above-mentioned steps, using rvetool ( Robotics Toolbox ) functions and show the animation of rotating frames step by step. A (0. 5.0) (0.3.3) (2,0.2) E (0.5.0) C DA (3,0,0) y Fig 2arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education