Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and... Problem 1.2P: How many outcome sequences are possible ten a die is rolled four times, where we say, for instance,... Problem 1.3P: Twenty workers are to be assigned to 20 different jobs, one to each job. How many different... Problem 1.4P: John, Jim, Jay, and Jack have formed a band consisting of 4 instruments if each of the boys can play... Problem 1.5P: For years, telephone area codes in the United States and Canada consisted of a sequence of three... Problem 1.6P: A well-known nursery rhyme starts as follows: As I was going to St. Ives I met a man with 7 wives.... Problem 1.7P: a. In how many ways can 3 boys and 3 girls sit in a row? b. In how many ways can 3 boys and 3 girls... Problem 1.8P: When all letters are used, how many different letter arrangements can be made from the letters a.... Problem 1.9P: A child has 12 blocks, of which 6 are black, 4 are red, 1 is white, and 1 is blue. If the child puts... Problem 1.10P: In how many ways can 8 people be seated in a row if a. there are no restrictions on the seating... Problem 1.11P: In how many ways can 3 novels. 2 mathematics books, and 1 chemistry book be arranged on a bookshelf... Problem 1.12P: How many 3 digit numbers zyz, with x, y, z all ranging from 0 to9 have at least 2 of their digits... Problem 1.13P: How many different letter permutations, of any length, can be made using the letters M 0 T T 0. (For... Problem 1.14P: Five separate awards (best scholarship, best leadership qualities, and so on) are to be presented to... Problem 1.15P: Consider a group of 20 people. If everyone shakes hands with everyone else, how many handshakes take... Problem 1.16P: How many 5-card poker hands are there? Problem 1.17P: A dance class consists of 22 students, of which 10 are women and 12 are men. If 5 men and 5 women... Problem 1.18P: A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How... Problem 1.19P: Seven different gifts are to be distributed among 10 children. How many distinct results are... Problem 1.20P: A committee of 7, consisting of 2 Republicans, 2 Democrats, and 3 Independents, is to be chosen from... Problem 1.21P: From a group of 8 women and 6 men, a committee consisting of 3 men and 3 women is to be formed. How... Problem 1.22P: A person has 8 friends, of whom S will be invited to a party. a. How many choices are there if 2 of... Problem 1.23P: Consider the grid of points shown at the top of the next column. Suppose that, starting at the point... Problem 1.24P: In Problem 23, how many different paths are there from A to B that go through the point circled in... Problem 1.25P: A psychology laboratory conducting dream research contains 3 rooms, with 2 beds in each room. If 3... Problem 1.26P: Show k=0n(nk)2k=3n Simplify k=0n(nk)xk Problem 1.27P: Expand (3x2+y)5. Problem 1.28P: The game of bridge is played by 4 players, each of w1om is dealt 13 cards. How many bridge deals are... Problem 1.29P: Expand (x1+2x2+3x3)4. Problem 1.30P: If 12 people are to be divided into 3 committees of respective sizes 3, 4, and 5, how many divisions... Problem 1.31P: If 8 new teachers are to be divided among 4 schools, how many divisions are possible? What if each... Problem 1.32P: Ten weight lifters are competing in a team weight-lifting contest. Of the lifters, 3 are from the... Problem 1.33P: Delegates from 10 countries, including Russia, France, England, and the United States, are to be... Problem 1.34P: If 8 identical blackboards are to be divided among 4 schools, how many divisions are possible? How... Problem 1.35P: An elevator starts at the basement with 8 people (not including the elevator operator) and... Problem 1.36P: We have 520.000 that must be invested among 4 possible opportunities. Each investment must be... Problem 1.37P: Suppose that 10 fish are caught at a lake that contains 5 distinct types of fish. a. How many... Problem 1.1TE: Prove the generalized version of the basic counting principle. Problem 1.2TE: Two experiments are to be performed. The first can result in any one of m possible outcomes. If the... Problem 1.3TE: In how many ways can r objects be selected from a set of n objects if the order of selection is... Problem 1.4TE: There are (nr) different linear arrangements of n balls of which r are black and nr are white. Give... Problem 1.5TE: Determine the number of vectors (x1,...,xn), such that each x1 is either 0 or 1 andi=1nxiK Problem 1.6TE: How many vectors x1,...,xk are there for which each xi is a positive integer such that1xin and... Problem 1.7TE: Give an analytic proof of Equation (4.1). Problem 1.8TE: Prove that (n+mr)=(n0)(mr)+(n1)(mr1)+...+(nr)(m0) Hint: Consider a group of n men and m women. How... Problem 1.9TE: Use Theoretical Exercise 8 I to prove that (2nn)=k=0n(nk)2 Problem 1.10TE: From a group of n people, suppose that we want to choose a committee of k,kn, one of whom is to be... Problem 1.11TE: The following identity is known as Fermats combinatorial identity:(nk)=i=kn(i1k1)nk Give a... Problem 1.12TE: Consider the following combinatorial identity: k=0nk(nk)=n2n1 a. Present a combinatorial argument... Problem 1.13TE: Show that, for n0 ,i=0n(1)i(ni)=0 Hint: Use the binomial theorem. Problem 1.14TE: From a set of n people, a committee of size j is to be chosen, and from this committee, a... Problem 1.15TE: Let Hn(n) be the number of vectors x1,...,xk for which each xi is a positive integer satisfying 1xin... Problem 1.16TE: Consider a tournament of n contestants in which the outcome is an ordering of these contestants,... Problem 1.17TE: Present a combinatorial explanation of why (nr)=(nr,nr) Problem 1.18TE: Argue that(nn1,n2,...,nr)=(n1n11,n2,...,nr)+(nn1,n21,...,nr)+...+(nn1,n2,...,nr1) Hint: Use an... Problem 1.19TE: Prove the multinomial theorem. Problem 1.20TE: In how many ways can n identical balls be distributed into r urns so that the ith urn contains at... Problem 1.21TE: Argue that there are exactly (rk)(n1nr+k) solutions of x1+x2+...+xr=n for which exactly k of the xi... Problem 1.22TE Problem 1.23TE: Determine the number of vectors (xi,...,xn) such that each xi, is a nonnegative integer and i=1nxik. Problem 1.1STPE: How many different linear arrangements are there of the letters A, B, C, D, E, F for which a. A and... Problem 1.2STPE: If 4 Americans, 3 French people, and 3 British people are to be seated in a row, how many seating... Problem 1.3STPE: A president. treasurer, and secretary. all different, are to be chosen from a club onsisting of 10... Problem 1.4STPE: A student is to answer 7 out of 10 questions in an examination. How many choices has she? How many... Problem 1.5STPE: In how many ways can a man divide 7 gifts among his 3 children if the eldest is to receive 3 gifts... Problem 1.6STPE: How many different 7-place license plates are possible mien 3 of the entries are letters and 4 are... Problem 1.7STPE: Give a combinatorial explanation of the identity(nr)=(nnr) Problem 1.8STPE: Consider n-digit numbers where each digit is one of the 10 integers 0,1, ... ,9. How many such... Problem 1.9STPE: Consider three classes, each consisting of n students. From this group of 3n students, a group of 3... Problem 1.10STPE: How many 5-digit numbers can be formed from the integers 1,2,... ,9 if no digit can appear more than... Problem 1.11STPE: From 10 married couples, we want to select a group of 6 people that is not allowed to contain a... Problem 1.12STPE: A committee of 6 people is to be chosen from a group consisting of 7 men and 8 women. If the... Problem 1.13STPE: An art collection on auction consisted of 4 Dalis, 5 van Goghs. and 6 Picassos, At the auction were... Problem 1.14STPE Problem 1.15STPE: A total of n students are enrolled in a review course for the actuarial examination in probability.... Problem 1.16STPE Problem 1.17STPE: Give an analytic verification of (n2)=(k2)+k(nk)+(n+k2),1kn. Now, give a combinatorial argument for... Problem 1.18STPE: In a certain community, there are 3 families consisting of a single parent and 1 child, 3 families... Problem 1.19STPE: If there are no restrictions on where the digits and letters are placed, how many 8-place license... Problem 1.20STPE: Verify the identityx1+...+xr=n,xi0n!x1!x2!...xr!=rn a. by a combinatorial argument that first notes... Problem 1.21STPE: Simplify n(n2)+(n3)...+(1)n+1(nn) format_list_bulleted

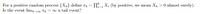
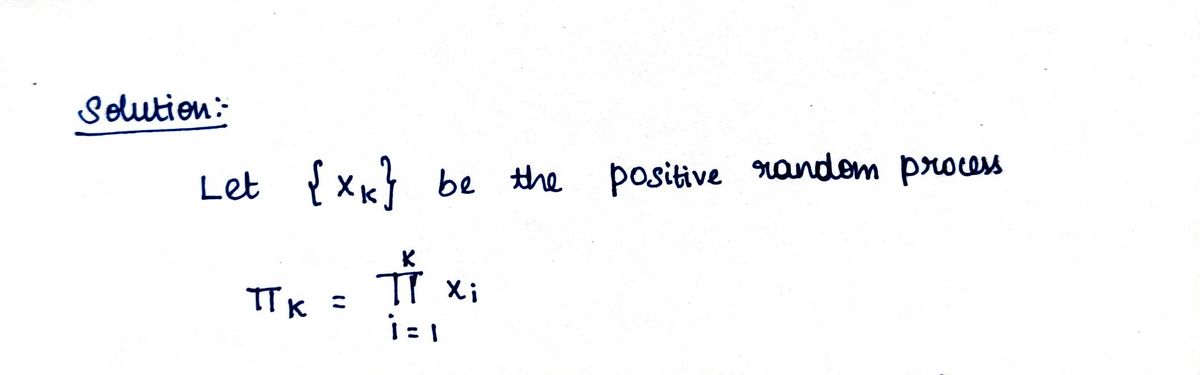

 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

