Related questions
I just need help with parts (f), (g), (h) and (i)
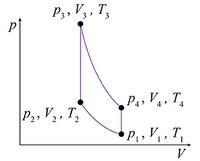
Problem 6: A certain gasoline engine is modeled as a monatomic ideal gas undergoing an Otto cycle, represented by the p-V diagram shown in the figure. The initial pressure, volume, and temperature are p1 = 0.95 × 105 Pa, V1 = 0.025 m3, and T1 = 310 K, respectively.
Part (a) Calculate the number of moles times the gas constant, nR, in joules per kelvin, to three significant figures, using the ideal-gas law and the initial values of pressure, volume, and temperature. This quantity will be useful for later calculations.
| nR = 7.7 |
Part (b) The first step in the Otto cycle is adiabatic compression. Enter an expression for the work performed on the gas during the first step, in terms of V1, V2, and p1.
| W1→2 = p1 V1 ( ( V1/V2 )( 2/3 ) - 1 )/( 2/3 ) |
Part (c) Calculate the work performed on the gas during the first step, in joules, for V2 = V1/6.2.
| W1→2 = 8460.58 |
Part (d) Calculate the temperature of the gas, in kelvins, at the end of the first step.
| T2 = 1046.2 |
Part (e) The second step in the Otto cycle is isochoric (constant-volume) heating. Calculate the heat absorbed by the gas during this process, in joules, if the temperature is increased so that T3 = 1.53T2.
| Qh = 6469 |
Part (f) Calculate the pressure at the end of the isochoric heating step, in pascals, to three significant figures.
Part (g) The third step in the Otto cycle is adiabatic expansion, which brings the volume back to its initial value. Calculate the work preformed on the gas, in joules, during the third step.
Part (h) The fourth and last step in the Otto cycle is isochoric cooling to the initial conditions. Find the amount of heat, in joules, that is discharged by the gas during the fourth step.
Part (i) Calculate the efficiency of this Otto cycle, expressed as a percent.
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 6 images
I don't understand how they got answers from part d and e.
I don't understand how they got answers from part d and e.
- A 2.00 mol sample of an ideal diatomic gas is taken through a reversible cycle A → B → C → A as shown in the figure below. Process A → B is isothermal expansion. For the cycle, calculate: a) the work done by the gas, b) the heat energy added to the gas, c) the heat energy exhausted by the gas, d) the thermal efficiency, e) the change in entropy of the gas. f) Determine the efficiency of a Carnot engine operating between the same temperature extremes, R = 8.314 J/mol K Data at vertices for the above PV diagram are as follow: PA = 5.00 x 105 Pa, VA = 1.00 x 10 -2 m3, PB = 1.25 x 105 Pa, VB = 4.00 x 10 -2 m3 PC = 1.25 x 105 Pa, VC = 1.00 x 10 -2 m3arrow_forwardExplain the heat transferred from a furnace (Q) to convert the boiler feed water at 25 ° C into superheated steam at 17 bar and 250 ° C.arrow_forwardPlease make sure to provide all the steps expecially for the question D. Thank you!arrow_forward
- I am getting lost in this practice problem for thermodynamics - thank you! Air at 100 kPa and 280K is compressed steadily to 600 kPa and 400K in an air compressor. The mass flow rate of air through the compressor is 0.02 kg/s and the compressor a heat loss of 16 kJ/kg from the compressor occurs. Assuming steady state steady flow conditions and ideal gas behavior (with constant specific heats, Cp=1.009 kJ/kgK, R=0.287 kJ/kgK, determine: a) The necessary power in put to the compressor(kW).b) The volumetric flow rate of air at the exit of the compressor (m3/s).arrow_forwardCan you provide the step-by-step solution how to get the answers? Steam flows adiabatically through a nozzle from 1517 KPaa, 290 °C, to 965 KPaa. Sketch the pV and Ts diagram and for m=454 gm/sec, Determine delta s, delta u, delta v, delta h, work nonflow and work steady flow. the first three (delta s, delta u, delta v, delta h) were already answered. Can you continue the bold partarrow_forwardHi I need help with parts of a thermo practice problem 2 kg of air in a piston cylinder initially at P1=101 kPa, T1= 300 K undergoes a cycle made up of three processes: 1-2 Isothermal compression until the volume is (1/15) of its original value.2-3 Constant Pressure heating3-1 Isentropic Expansion back to the initial state Assume air is an ideal gas with constant specific heats with the following values: Cpo=1.027kJ/kgK; Cvo= 0.740 kJ/kgK; R=0.287 kJ/kgK; ɣ=1.388 Fill in the processes table below and show all work.arrow_forward
- Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education 
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY