
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
Please show free body diagram
a and b
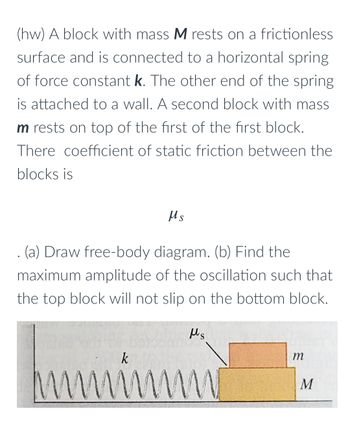
Transcribed Image Text:### Problem Statement
A block with mass \( M \) rests on a frictionless surface and is connected to a horizontal spring of force constant \( k \). The other end of the spring is attached to a wall. A second block with mass \( m \) rests on top of the first block. The coefficient of static friction between the blocks is \( \mu_s \).
#### Tasks:
1. **Draw a free-body diagram.**
2. **Find the maximum amplitude of the oscillation such that the top block will not slip on the bottom block.**
### Free-Body Diagram
Below is the description of the free-body diagram shown in the image:
1. The figure depicts two blocks, one with mass \( M \) (bottom block) and one with mass \( m \) (top block).
2. The bottom block \( M \) is connected to a spring with spring constant \( k \).
3. The surface on which block \( M \) rests is frictionless.
4. The coefficient of static friction between the blocks is denoted by \( \mu_s \).
5. The top block \( m \) is subjected to frictional force due to the coefficient of static friction \( \mu_s \), preventing it from slipping off the bottom block during oscillations.
### Detailed Explanation of the Diagram:
- **Spring:** A horizontal spring is attached to a wall at one end and to the bottom block \( M \) at the other end. The spring is shown in a compressed or stretched state, indicating its oscillatory motion potential.
- **Blocks:** The bottom block \( M \) is in direct contact with the frictionless surface, whereas the top block \( m \) is placed on the bottom block \( M \).
- **Friction:** The static friction between blocks \( m \) and \( M \) is represented by \( \mu_s \), preventing the top block from slipping when oscillated horizontally.
### Mathematical Formulation
#### (a) Free-Body Diagram:
- **For the top block (m):**
- Weight (\( mg \)) acts downward.
- Normal force (\( N \)) acts upward.
- Frictional force (\( f = \mu_s \cdot N \)) acts horizontally to the left or right, opposing motion relative to the bottom block.
- **For the bottom block (M):**
- Weight (\( Mg \)) and the normal reaction from
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Two blocks are connected by a massless rope. The rope passes over an ideal (frictionless and massless) pulley such that one block with mass m1 = 12.25 kg is on a horizontal table and the other block with mass m2 = 7.5 kg hangs vertically. Both blocks experience gravity and the tension force, T. Use the coordinate system specified in the diagram. a.) Assuming friction forces are negligible, write an expression, using only the variables provided, for the acceleration that the block of mass m1 experiences in the x-direction. Your answer should involve the tension, T. b.) Under the same assumptions, write an expression for the acceleration, a2, the block of mass m2 experiences in the y-direction. Your answer should be in terms of the tension, T and m2. c.) Carefully consider how the accelerations a1 and a2 are related. Solve for the magnitude of the acceleration, a1, of the block of mass m1, in meters per square second. d.)Find the magnitude of the tension in the rope, T, in newtons.arrow_forwardAlso draw the free body diagram for Block A and Block Barrow_forwardSet up the free-body diagram and equations for Newton's 2nd law for each object along each axis. Assume friction is present between all surfaces and the coefficient of friction is different between the different surfaces. (Note you should have 2 free body diagrams) A B Horizontal table Pullarrow_forward
- In , the man has a mass of 65 kg and the crate has a mass of 110 kg. The coefficient of static friction between his shoes and the ground is μs = 0.4 and between the crate and the ground is μc = 0.3. A) Determine if the man is able to move the crate using the rope-and-pulley system shown. B) Prove your answer to part A by calculating the static frictional force F�between the man's shoes and the ground required to move the crate and the maximum static frictional force Fmax which can be developed. Express your answers in newtons to three significant figures separated by a com_ma.arrow_forwardConsider the system in the picture below: a cart of mass M with a static friction coefficient u is connected through a massless string to a hanging mass m. M is a capital letter, m is lower case. Write them as such, or vour equations will be confusing, M We want to find the maximum value of the hanging mass m such that the system is in equilibrium. 1. Free body diagram (FBD): Draw a FBD for each: the Cart and the hanging mass. Clearly show all the forces. 2. Clearly write the equilibrium equations for the cart in the horizontal and vertical direction. 3. Clearly write the equilibrium equation for the hanging mass. 4. Solve the system of the three equations above for the hanging mass m. Show your calculation to get credit. 5. What would happen if mass m exceeds this value? Explain.arrow_forwardCrate A hangs from a cable C and rests against the wall, so that the cable makes an angle with the wall. Draw a complete free-body diagram of crate A. Include labeledangle(s), in terms of ?, for any force(s) that are at an angle (not purely horizontal or vertical).arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON