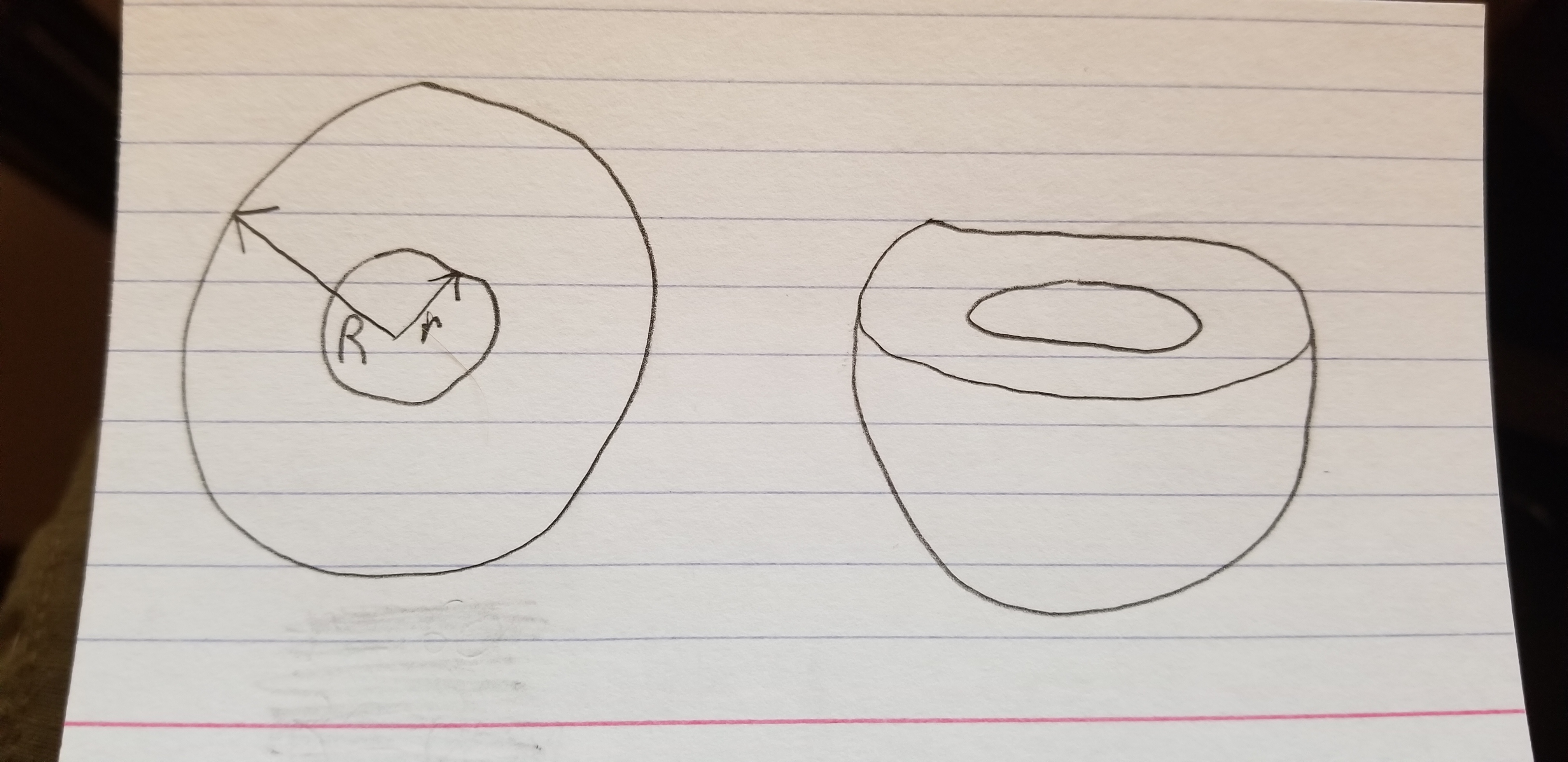
How do I find the density of a hemispherical bowl floating in water? The bowls top is perfectly in line with the water so no water is inside the bowl. The inner radius is r=6cm and the outer radius is R=8cm. (I know the density of water is 1000kg/m^3 and I found the volume of the bowl as V=619.94cm^3 using the formula 2/3*pi*(R-r).) But I am having difficulty after this. I believe I should use the buoyancy formula F=p*g*V but I am not sure. Also, if I do use that formula, if buoyancy formula is equal to the weight of the water displaced, then how do I use that to find the density of the object? Please let me know if I am doing this correctly so far and how I proceed. Also please show me step by step how you solve this because I am still learning Archimedes Principle and such. (sorry for crappy illustration, I am by no means an artist)
Step by stepSolved in 2 steps with 1 images

- Bowling balls are roughly the same size but come in a variety of weights. Given that the official radius a bowling ball should have is roughly 0.111 m, calculate the weight of the heaviest bowling ball that will float in a fluid of density 1.100 × 10° kg/m³. weight: Narrow_forwardThe density of a composite is 1.7 g/cm3. The density of an unknown fluid is 2.2 g/cm3. An object made of the composite will _____ in the unknown fluid.arrow_forwardYou put a marble on a balance and find it has a mass of 1.2 grams. It is an irregular shape, so you need to do displacement to find its volume. You put it in a graduated cylinder with a starting volume of 30.0 mL of water. After you add the marble, the water rises to 31.5 mL. What is the density? Group of answer choices 0.038 g/mL 1.3 g/mL 0.80 g/mL 1.8 g/mLarrow_forward