
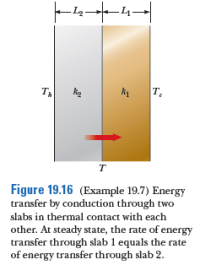
Two slabs of thickness L1 and L2 and thermal conductivities k1 and k2 are in thermal contact with each other as shown. The temperatures of their outer surfaces are Tc and Th, respectively, and Th >Tc. Determine the temperature at the interface and the rate of energy transfer by
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

In the question its asks for the rate of energy transfer P after you find what the interface temperature T is.
Upon completion from submitting T in into the intial rate equation the final expansion gives:
P = A(Th - Tc) / (L1/ k1) + (L2/ k2)
I understand how T was achieved from expanding the P1 = P2 substitution, but how is P found from inserting T into P1 = k1A (T - Tc / L1)?
Hello, I am still confused on the second part of this question, how you find the rate of energy transfer by inserting what T is into one of the initial equations:
P1 = k1A (T - Tc / L1)
Could you show the worked out procedure as you did for finding T please?
In the question its asks for the rate of energy transfer P after you find what the interface temperature T is.
Upon completion from submitting T in into the intial rate equation the final expansion gives:
P = A(Th - Tc) / (L1/ k1) + (L2/ k2)
I understand how T was achieved from expanding the P1 = P2 substitution, but how is P found from inserting T into P1 = k1A (T - Tc / L1)?
Hello, I am still confused on the second part of this question, how you find the rate of energy transfer by inserting what T is into one of the initial equations:
P1 = k1A (T - Tc / L1)
Could you show the worked out procedure as you did for finding T please?
- The thermal conductivities of human tissues vary greatly. Fat and skin have conductivities of about 0.20 W/m · K and 0.020 W/m · K respectively, while other tissues inside the body have conductivities of about 0.50 W/m · K. Assume that between the core region of the body and the skin surface lies a skin layer of 1.0 mm, fat layer of 0.50 cm, and 3.2 cm of other tissues. (a) Find the R-factor for each of these layers, and the equivalent R-factor for all layers taken together, retaining two digits. Rskin m2 · K/W Rfat m2 · K/W Rtissue m2 · K/W R m2 · K/W (b) Find the rate of energy loss when the core temperature is 37°C and the exterior temperature is 0°C. Assume that both a protective layer of clothing and an insulating layer of unmoving air are absent, and a body area of 2.0 m2. Warrow_forwardAn insulated container contains two moles of an ideal gas at atmospheric pressure. Keeping the pressure constant, if the temperature of the gas is increased by 50 °C, then its volume increases by 400 cm3 and if the temperature is increased by 100 °C, then its volume increases by 600 cm³. Determine the initial volume and temperature of the gas. (Write the equation of ideal gas initially, after the temperature increase of 50 °C, and after increase of temperature by 100 °C. Combine these three equations to find the initial volume and temperature)arrow_forwardA silver block, initially at 56.9 ∘C∘C, is submerged into 100.0 gg of water at 24.1 ∘C∘C, in an insulated container. The final temperature of the mixture upon reaching thermal equilibrium is 27.4 ∘C∘C. What is the mass of the silver block? Express your answer to two significant figures and include the appropriate units.arrow_forward
- On a chilly 10°C day, you quickly take a deep breath—all your lungs can hold, 4.0 L. The air warms to your body temperature of 37°C. If the air starts at a pressure of 1.0 atm, and you hold the volume of your lungs constant (a good approximation) and the number of molecules in your lungs stays constant aswell (also a good approximation), what is the increase in pressure inside your lungs?arrow_forwardInterstellar space is quite different from the gaseous environments we commonly encounter on Earth. For instance, a typical density of the medium is about 1 atom cm−3 and that atom is typically H; the effective temperature due to stellar background radiation is about 10 kK. Estimate the diffusion coefficient and thermal conductivity of H under these conditions. Compare your answers with the values for gases under typical terrestrial conditions. Comment: Energy is in fact transferred much more effectively by radiation.arrow_forward2.00 mol of helium and 1.00 mol of argon are separated by a very thin barrier. Initially the helium has 7500 J of thermal energy. The helium gains 2500 J of energy as the gases interact and come to thermal equilibrium by exchanging energy via collisions at the boundary. What was the initial temperature of the argon? First, what is the equilibrium temperature of the two gases? Express your answer in kelvins. ► View Available Hint(s) Tf = Submit Part B VE ΑΣΦ help What is the thermal energy of the argon at the equilibrium temperature? Express your answer with the appropriate units.arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





