
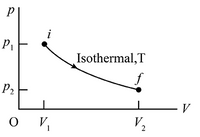
Consider a cylinder with a movable piston containing n moles of an ideal gas. The entire apparatus is immersed in a constant temperature bath of temperature T Kelvin. The piston pushes slowly outward on an external body which matches the force momentarily at each instant so that the gas expands quasi-statically from a volume V1 to V2 at constant temperature T. The isothermal process is shown in the figure above, where the pressure p is related to the volume V by the
pV = nRT, where R is the gas constant.
Q: For n = 3 moles, T = 310 K, and V2 = 3.5V1, determine the work done by the gas on the external body. The gas constant is R = 8.314 J K-1 mol-1.
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

- Please help mearrow_forwardConsider a process that uses n moles of a monatomic ideal gas operating through a Carnot cycle. The initial temperature and pressure of the gas are T1 and P1, respectively. Consider steps 1 → 2, 2 → 3, 3 → 4, and 4 → 1. Write an expression for the volume V4 in terms of V1. Write an expression for P4 in terms of n, R, T4 and V4.arrow_forwardIn an isochoric process, one mole of an ideal gas of rigid diatomic molecules at volume V is taken from an initial temperature T to a final temperature 4T. Using the convention that heat is positive when it is absorbed by the system, what is the heat transfer in terms of R and T?arrow_forward
- A container is filled with an ideal diatomic gas to a pressure and volume of P1 and V1, respectively. The gas is then warmed in a two-step process that increases the pressure by a factor of five and the volume by a factor of four. Determine the amount of energy transferred to the gas by heat if the first step is carried out at constant volume and the second step at constant pressure. (Use any variable or symbol stated above as necessary.)arrow_forwardProblem #2: For this problem, one mole of a diatomic ideal gas is taken around a reversible cycle by starting at pressure P, volume V, and temperature T, then in an isochoric process 1 increasing pressure to 6P, then in an isobaric process 2 increasing its volume to 21V, then another isochoric process 3 back to a pressure P, and finally in an isobaric process 4 back to P, V, T. Find the temperature of this gas at the end of process 1, 2, and 3 in terms of the original temperature T. Find the internal energy change in process 1 and in process 2 in terms of P and V. Find the heat transfer in process 1 and in process 2 in terms of P and V.arrow_forwardProblem 4: Consider a cylinder with a movable piston containing n moles of an ideal gas. The entire apparatus is immersed in a constant temperature bath of temperature T Kelvin. The piston pushes slowly outward on an external body which matches the force momentarily at each instant so that the gas expands quasi-statically from a volume V1 to V2 at constant temperature T. The isothermal process is shown in the figure above, where the pressure p is related to the volume V by the ideal gas law as follows: pV = nRT, where R is the gas constant. Part (b) For n = 3 moles, T = 350 K, and V2 = 2.5V1, determine the work done by the gas on the external body. The gas constant is R = 8.314 J K-1 mol-1.arrow_forward
- An ideal monatomic gas undergoes changes in pressure and volume, as shown in the pV diagram below. The initial volume is 0.02 m3 and the final volume is 0.10 m3. The initial pressure is 1 atm and the final pressure is 2 atm. Recall that 1 atm = 101.3 kPa. (a) Calculate the magnitude, or absolute value, of the work done on the gas in this process. Answer = - 13429J (c) The initial temperature of the gas is 308 K. Calculate the temperature of the gas at the end of the process. Answer = 3080 k Just need answer with the following: (d) What is the change in thermal energy for the gas in this process? (e) Calculate the quantity of heat transfer added to (positive) or removed from (negative) the gas during this process.arrow_forwardA particular thermodynamic cycle acting on a monatomic ideal gas (y = 1.67) includes an isobaric expansion, an isochoric cooling, and then a isothermic contraction. The PV diagram is shown in the image below. P V The isobaric expansion occurs at a pressure of 2.265 × 105 Pa and changes the volume of the gas from 5.9 × 10 2 m³ to 10.98 × 10-2 m³. What is the efficiency of the process?arrow_forwardThe graph shown is for a dilute gas that follows the clockwise path of quasi-static steps: isobaric expansion, isochoric reduction of pressure, isobaric compression, and isochoric increase in pressure. The vertical axis is shown in multiples of the pressure pp, where p=2.5atm, and the horizontal axis is shown in multiples of V, where V=4L. Part (a) What is the work done for the segment from state A to state B? Part (b) What is the work done for the segment from state B to state C? Part (c) What is the work done for the segment from state C to state D? Part (d) What is the total work done in making a single clockwise cycle, A to B to C to D?arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





