
Practical Management Science
6th Edition
ISBN: 9781337406659
Author: WINSTON, Wayne L.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
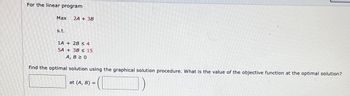
Transcribed Image Text:For the linear program
Max
s.t.
2A + 3B
1A + 2B ≤ 4
5A + 38 ≤ 15
A, B 2 0
find the optimal solution using the graphical solution procedure. What is the value of the objective function at the optimal solution?
at (A, B) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 14 images

Knowledge Booster
Similar questions
- The method for rating teams in Example 7.8 is based on actual and predicted point spreads. This method can be biased if some teams run up the score in a few games. An alternative possibility is to base the ratings only on wins and losses. For each game, you observe whether the home team wins. Then from the proposed ratings, you predict whether the home team will win. (You predict the home team will win if the home team advantage plus the home teams rating is greater than the visitor teams rating.) You want the ratings such that the number of predictions that match the actual outcomes is maximized. Try modeling this. Do you run into difficulties? (Remember that Solver doesnt like IF functions.) EXAMPLE 7.8 RATING NFL TEAMS9 We obtained the results of the 256 regular-season NFL games from the 2015 season (the 2016 season was still ongoing as we wrote this) and entered the data into a spreadsheet, shown at the bottom of Figure 7.38. See the file NFL Ratings Finished.xlsx. (Some of these results are hidden in Figure 7.38 to conserve space.) The teams are indexed 1 to 32, as shown at the top of the sheet. For example, team 1 is Arizona, team 2 is Atlanta, and so on. The first game entered (row 6) is team 19 New England versus team 25 Pittsburgh, played at New England. New England won the game by a score of 28 to 21, and the point spread (home team score minus visitor team score) is calculated in column J. A positive point spread in column J means that the home team won; a negative point spread indicates that the visiting team won. The goal is to determine a set of ratings for the 32 NFL teams that most accurately predicts the actual outcomes of the games played.arrow_forwardReferring to Example 11.1, if the average bid for each competitor stays the same, but their bids exhibit less variability, does Millers optimal bid increase or decrease? To study this question, assume that each competitors bid, expressed as a multiple of Millers cost to complete the project, follows each of the following distributions. a. Triangular with parameters 1.0, 1.3, and 2.4 b. Triangular with parameters 1.2, 1.3, and 2.2 c. Use @RISKs Define Distributions window to check that the distributions in parts a and b have the same mean as the original triangular distribution in the example, but smaller standard deviations. What is the common mean? Why is it not the same as the most likely value, 1.3?arrow_forwardIf a monopolist produces q units, she can charge 400 4q dollars per unit. The variable cost is 60 per unit. a. How can the monopolist maximize her profit? b. If the monopolist must pay a sales tax of 5% of the selling price per unit, will she increase or decrease production (relative to the situation with no sales tax)? c. Continuing part b, use SolverTable to see how a change in the sales tax affects the optimal solution. Let the sales tax vary from 0% to 8% in increments of 0.5%.arrow_forward
- Assume the demand for a companys drug Wozac during the current year is 50,000, and assume demand will grow at 5% a year. If the company builds a plant that can produce x units of Wozac per year, it will cost 16x. Each unit of Wozac is sold for 3. Each unit of Wozac produced incurs a variable production cost of 0.20. It costs 0.40 per year to operate a unit of capacity. Determine how large a Wozac plant the company should build to maximize its expected profit over the next 10 years.arrow_forwardIn Example 11.3, suppose you want to run five simulations, where the probability of passing inspection is varied from 0.6 to 1.0 in increments of 0.1. Use the RISKSIMTABLE function appropriately to do this. Comment on the effect of this parameter on the key outputs. In particular, does the probability of passing inspection have a large effect on when production should start? (Note: When this probability is low, it might be necessary to produce more than 25 batches, the maximum built into the model. Check whether this maximum should be increased.)arrow_forwardLemingtons is trying to determine how many Jean Hudson dresses to order for the spring season. Demand for the dresses is assumed to follow a normal distribution with mean 400 and standard deviation 100. The contract between Jean Hudson and Lemingtons works as follows. At the beginning of the season, Lemingtons reserves x units of capacity. Lemingtons must take delivery for at least 0.8x dresses and can, if desired, take delivery on up to x dresses. Each dress sells for 160 and Hudson charges 50 per dress. If Lemingtons does not take delivery on all x dresses, it owes Hudson a 5 penalty for each unit of reserved capacity that is unused. For example, if Lemingtons orders 450 dresses and demand is for 400 dresses, Lemingtons will receive 400 dresses and owe Jean 400(50) + 50(5). How many units of capacity should Lemingtons reserve to maximize its expected profit?arrow_forward
- The annual demand for Prizdol, a prescription drug manufactured and marketed by the NuFeel Company, is normally distributed with mean 50,000 and standard deviation 12,000. Assume that demand during each of the next 10 years is an independent random number from this distribution. NuFeel needs to determine how large a Prizdol plant to build to maximize its expected profit over the next 10 years. If the company builds a plant that can produce x units of Prizdol per year, it will cost 16 for each of these x units. NuFeel will produce only the amount demanded each year, and each unit of Prizdol produced will sell for 3.70. Each unit of Prizdol produced incurs a variable production cost of 0.20. It costs 0.40 per year to operate a unit of capacity. a. Among the capacity levels of 30,000, 35,000, 40,000, 45,000, 50,000, 55,000, and 60,000 units per year, which level maximizes expected profit? Use simulation to answer this question. b. Using the capacity from your answer to part a, NuFeel can be 95% certain that actual profit for the 10-year period will be between what two values?arrow_forwardAlthough the normal distribution is a reasonable input distribution in many situations, it does have two potential drawbacks: (1) it allows negative values, even though they may be extremely improbable, and (2) it is a symmetric distribution. Many situations are modelled better with a distribution that allows only positive values and is skewed to the right. Two of these that have been used in many real applications are the gamma and lognormal distributions. @RISK enables you to generate observations from each of these distributions. The @RISK function for the gamma distribution is RISKGAMMA, and it takes two arguments, as in =RISKGAMMA(3,10). The first argument, which must be positive, determines the shape. The smaller it is, the more skewed the distribution is to the right; the larger it is, the more symmetric the distribution is. The second argument determines the scale, in the sense that the product of it and the first argument equals the mean of the distribution. (The mean in this example is 30.) Also, the product of the second argument and the square root of the first argument is the standard deviation of the distribution. (In this example, it is 3(10=17.32.) The @RISK function for the lognormal distribution is RISKLOGNORM. It has two arguments, as in =RISKLOGNORM(40,10). These arguments are the mean and standard deviation of the distribution. Rework Example 10.2 for the following demand distributions. Do the simulated outputs have any different qualitative properties with these skewed distributions than with the triangular distribution used in the example? a. Gamma distribution with parameters 2 and 85 b. Gamma distribution with parameters 5 and 35 c. Lognormal distribution with mean 170 and standard deviation 60arrow_forwardIn Example 11.1, the possible profits vary from negative to positive for each of the 10 possible bids examined. a. For each of these, use @RISKs RISKTARGET function to find the probability that Millers profit is positive. Do you believe these results should have any bearing on Millers choice of bid? b. Use @RISKs RISKPERCENTILE function to find the 10th percentile for each of these bids. Can you explain why the percentiles have the values you obtain?arrow_forward
- You want to take out a 450,000 loan on a 20-year mortgage with end-of-month payments. The annual rate of interest is 3%. Twenty years from now, you will need to make a 50,000 ending balloon payment. Because you expect your income to increase, you want to structure the loan so at the beginning of each year, your monthly payments increase by 2%. a. Determine the amount of each years monthly payment. You should use a lookup table to look up each years monthly payment and to look up the year based on the month (e.g., month 13 is year 2, etc.). b. Suppose payment each month is to be the same, and there is no balloon payment. Show that the monthly payment you can calculate from your spreadsheet matches the value given by the Excel PMT function PMT(0.03/12,240, 450000,0,0).arrow_forwardIn the lawn mower production problem in Example 8.4, experiment with the penalty cost for unsatisfied pickups in week 1. If this cost is sufficiently small, does the company ever produce fewer than seven models in week 1 and allow some week 1 pickups to be unsatisfied?arrow_forwardIn Example 11.3, if a batch fails to pass inspection, the entire batch is unusable. Change the model so that if a batch fails to pass inspection, it is reworked, and at the end of the rework, its entire yield (the same yield determined in column C) is usable. However, the rework takes 3, 4, or 5 days with respective probabilities 0.2, 0.5, and 0.3. Run the simulation for the modified model and comment on how the results change.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,