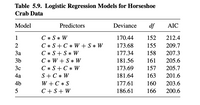
For the horseshoe crab data with width, color, and spine as predictors, suppose you start a backward elimination process with the most complex model possible. Denoted by C ∗ S ∗ W, it uses main effects for each term as well as the three two-factor interactions and the three-factor interaction. Table 5.9 shows the fit for this model and various simpler models. a. Conduct a likelihood-ratio test comparing this model to the simpler model that removes the three-factor interaction term but has all the two-factor interactions. Does this suggest that the three-factor term can be removed from the model? b. At the next stage, if we were to drop one term, explain why we would select model C ∗ S + C ∗ W. c. For the model at this stage, comparing to the model S + C ∗ W results in an increased deviance of 8.0 on df = 6 (P = 0.24); comparing to the model W + C ∗ S has an increased deviance of 3.9 on df = 3 (P = 0.27). Which term would you take out?

A random sample of eight drivers selected from a small town insured with a company and having similar minimum required auto insurance policies was selected. The following table lists their driving experiences in years and monthly auto insurance premiums in dollars.    Driving Experience:             5      2      12      9      15      6      25      16 Monthly Premium in $:     64    87    50     71     44     56     42      60   We are creating a regression model (line) to predict premium amount using driving experience.   A. Identify the Dependent and Independent variables. B. Using Excel, create a regression output page. Attach the output page. C. Complete the regression line. D. Evaluate and explain the strength of the relationship. E. How good is the model according to the Coefficient of Determination? F. Predict the premium when the driving experience is 8 years. G. Predict the premium when the driving experience is 18 years.

a. Give the design​ matrix, the observation​ vector, and the unknown parameter vector. Choose the correct design matrix X below. b. Find the associated least-squares curve for the data

The Pilot Pen Company has decided to use 15 test markets to examine the sensitivity of demand for its new product to various prices, as shown in the following table. Advertising effort was identical in each market. Each market had approximately the same level of business activity and population. Complete the following worksheet and then estimate the demand function for Pilot's new pen using a linear regression model. Test Market i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Total O 1.577 Regression Parameters Estimations Slope (B) Intercept (a) O 1.761 O 105.432 O 0.028 Price Charged (cents) Xi 50 50 55 55 60 60 65 65 70 70 80 80 90 90 40 1.902 O 0.032 980 What is the standard error of the estimate (se)? Quantity Sold (Thousands of Pens) O Yes O No Yi 20 21 19 19.5 20.5 19 16.5 15 14 15.5 13 14 11.5 11 17 What is the estimate of the standard deviation of the estimated slope (st)? 246.5 TiYi 1,000 1,050 1,045 1,072.5 1,230 1,140 1,072.5 975 980 1,085 1,040 1,120 1,035 990 680 I₂² 2,500 2,500…

Which of the following is/are the assumptions of linear models:. The response variable is normally distributed The residuals are normally distributed All the observed units are independent from each other. The relationship between the response variable and the predictors are linear All of the above None of the above.

O 4G ! 9:7 A moodle1.du.edu.om The following table shows trip generation data. Estimate b1 and b2 parameters using Regression method. Y=b1+b2 X HH No. Trips/day 4 3 10 4 13 16 17 20 8 19 19 20 Select one: O a. b1=4.78 and b2=8.76 b. b1=4.2 and b2=2.76 c. b1=7.3 and b2=5.66 d. b1=3.53 and b2=1.98 II

Mark Gershon, owner of a musical instrument distributorship, thinks that demand for guitars may be related to the number of television appearances by the popular group Maroon 5 during the previous month. Gershon has collected the data shown in the following table: Maroon 5 TV Appearances Demand for Guitars 3 4 5 8 6 5 9 6 8 8 6 9 This exercise contains only parts b, c, and d. b) Using the least-squares regression method, the equation for forecasting is (round your responses to four decimal places): Y=0+0x