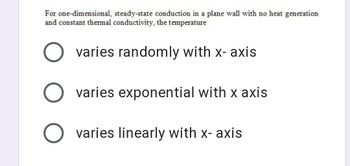
For one-dimensional, steady-state conduction in a plane wall with no heat generation and constant thermal conductivity, the temperature O varies randomly with x-axis O varies exponential with x axis O varies linearly with x-axis

You can in handwritten also. A circular (annular) fin of radius r2 is attached to a pipe of radius r1. The fin is exposed to an ambient fluid at temperature T∞ having heat transfer coefficient h and the fin base is maintained at temperature Tb. The fin thickness (t) is small compared to the fin length and the heat loss from the fin tip can be considered negligible compared with that from the top and bottom surfaces of the fin. Derive the differential equation and the boundary conditions for this fin by writing an energy balance around a differential volume element. Write your assumptions in detail. Do not solve the differential equation.

The exposed surface (x = 0) of a planar wall of thermal conductivity k is subject to microwave radiation that causes the volumetric heating to vary as: q ̇ (x) = q ̇o (1-x / L) Where qo (W / m ^ 3) is a constant. The boundary of x = L is well insulated, while the exposed surface is kept at a constant temperature T0. Determine the temperature distribution T (x) in terms of x, L, k, q ̇o, and T0.     in the attached image it is in Spanish

Consider a 2-ft * 2-ft thin square plate in a room at 75°F. One side of the plate is maintained at a temperature of 130°F, while the other side is insulated. Determine the rate of heat transfer from the plate by natural convection if the plate is (a) vertical, (b) horizontal with hot surface facing up, and (c) horizontal with hot surface facing down.

A steel sphere of diameter d and thermal conductivity k is being cooled in a flowing stream of air of bulk temperature T. The temperature distribution in the ball at a particular instant can be approximated as T- a + br + crª, where a, b and c are functions of time, and I is in K. What is the surface heat transfer coefficient? What is the unit of b?

Consider a cylindrical cavity of diameter D =100 mm and depth L = 10 mm whose sidewall and bottom are diffuse and gray with an emissivity of 0.6 and are at a uniform temperature of 1500 K. The top of the cavity is open and exposed to surroundings that are large and at 300 K. (a) Calculate the net radiation heat transfer rate from the cavity, in W, treating the bottom and sidewall of the cavity as one surface. (b) Calculate the net radiation heat transfer rate from the cavity, in W, treating the bottom and sidewall of the cavity as two separate surfaces.