Question
For a certain system, the operator corresponding to the quantity Aˆ does not commute with the Hamiltonian and also
has eigenvalues a1, a2 and eigenfunctions
respectively, where | u1⟩ and | u2⟩ are eigenfunctions of the Hamiltonian with eigenvalues E1 and E2.
a) If at time t = 0 the system is in the state | φ1⟩, show that the expected value of Aˆ at time t is
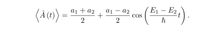
Transcribed Image Text:a1 + a2
а1 — а2
Cos
E1 – E2
-
-t
2

Transcribed Image Text:|u1) + |u2).
V2
|u1) – |u2)
-
|ø1) :
|#2) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Suppose that you have the Lagrangian L = (;2 + ʻr²) + 20 for a 2D 20 system in plane polar coordinates (r, 0). Determine the Hamiltonian.arrow_forwardPart barrow_forwardFor a one dimensional system, x is the position operator and p the momentum operator in the x direction.Show that the commutator [x, p] = iharrow_forward
- The Hamiltonian matrix has been constructed using an orthonormal basis. (1 1 0V (1 0 1) A = (2 1 0 )+(0 2 2 \2 1 4 where H = Hº + V and cis a constant. 1 2 0/ b) Use time-independent perturbation theory to determine the eigenvalues with corrections up to second order.arrow_forwardEvaluate the commutator [Â,B̂] of the following operators.arrow_forward
arrow_back_ios
arrow_forward_ios