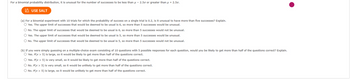
For a binomial probability distribution, it is unusual for the number of successes to be less than μ-2.50 or greater than + 2.50. USE SALT (a) For a binomial experiment with 10 trials for which the probability of success on a single trial is 0.2, is it unusual to have more than five successes? Explain. O Yes. The upper limit of successes that would be deemed to be usual is 6, so more than 5 successes would be unusual. O No. The upper limit of successes that would be deemed to be usual is 6, so more than 5 successes would not be unusual. O Yes. The upper limit of successes that would be deemed to be usual is 5, so more than 5 successes would be unusual. O No. The upper limit of successes that would be deemed to be usual is 5, so more than 5 successes would not be unusual. (b) If you were simply guessing on a multiple-choice exam consisting of 10 questions with 5 possible responses for each question, would you be likely to get more than half of the questions correct? Explain. O Yes. P(x > 5) is large, so it would be likely to get more than half of the questions correct. O Yes. P(x > 5) is very small, so it would be likely to get more than half of the questions correct. O No. P(x > 5) is very small, so it would be unlikely to get more than half of the questions correct. O No. P(x > 5) is large, so it would be unlikely to get more than half of the questions correct.

A Binomial experiment has 100 trials and a probability of success of 0.8.Determine the mean of this experiment.

Millo.09.

For a binomial distribution, which probability is not equal to the probability of 1 success in 7 trials where the probability of success is 0.277? Select one: Probability of 6.000 failures in 7 trials where the probability of success is 0.723 Probability of 1 success in 7 trials where the probability of failure is 0.723 Probability of 6.000 failures in 7 trials where the probability of failure is 0.723 Probability of 6.000 failures in 7 trials where the probability of success is 0.277 ( don't hand writing solution)

Suppose that 70% of Americans support the death penalty for persons convicted of murder. Let p> (p hat) be the sample proportion of proportion of people who support the death penalty in an SRS of Americans.  Suppose we set our sample size to be n=84. What is the probability of choosing an SRS in which between 65% and 73% of the people in the people in the sample support the death penalty? That is, find P(0.65<p(phat)<0.73). Show your work and box your answer.

A doctor is interested in the proportion of patients which live at least 5 years after being diagnosed with stage 4 breast cancer. He randomly selects 138 patients diagnosed with stage 4 breast cancer and follows them for 5 years. Suppose the true 5 year survival rate for stage 4 breast cancer is 38%. 1. How are the collection of all sample proportions of samples of size 138 distributed? NO 2. What is the probability that fewer than 34% of the patients studied survived for at least 5 years? o List the z-scores needed to calculate the result. If there is more than one z-score, separate the values with a comma. o There is a survived for at least 5 years. 3. What is the probability that more than 45% of the patients studied survived for at least 5 years? chance that fewer than 34% of the patients studied o List the z-scores needed to calculate the result. If there is more than one z-score, separate the values with a comma. O There is a survived for at least 5 years. chance that more than…