Question
Find V(t) for t>=0
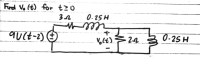
Transcribed Image Text:### Educational Explanation: Analyzing an RL Circuit with a Step Function Voltage Source
#### Problem Statement:
The objective is to find \( V_o(t) \) for \( t \geq 0 \).
#### Circuit Description:
The given circuit features the following components and configuration:
- A voltage source of 9 times the unit step function, \( 9U(t-2) \), is connected in series.
- A 3-ohm resistor (\( 3 \Omega \)) is connected in series with the voltage source.
- Following the resistor is an inductor with an inductance of 0.25 Henry (\( 0.25 H \)).
- This series combination is then connected to a parallel combination that includes:
- A 2-ohm resistor (\( 2 \Omega \))
- Another inductor with the same inductance of 0.25 Henry (\( 0.25 H \))
The circuit forms a series-parallel RL configuration.
#### Step-by-Step Analysis:
1. **Identify the Key Variables**:
- **Current through the circuit**.
- **Voltage across the inductors**.
2. **Analyze the Impact of the Step Input**:
- The voltage source \( 9U(t-2) \) implies a step function that turns on at \( t = 2 \) with a magnitude of 9V.
- For \( t < 2 \), the voltage source is 0V.
- For \( t \geq 2 \), the voltage source is 9V.
3. **Write the Differential Equations**:
- The impedance of the inductors needs to be considered.
- Initially assume steady-state solutions to find initial conditions and then solve using Laplace transforms or classical methods.
4. **Calculation and Simplification**:
- Translate the circuit into the Laplace domain to simplify the differential equations.
- Solve for \( V_o(s) \) and then perform the inverse Laplace transform to find \( V_o(t) \).
5. **Initial and Final Conditions**:
- At \( t = 0 \), everything behaves as if the circuit has been at rest for a long period.
- Evaluate the current and voltage for both resistors and inductors at \( t = 2 \), just before and after the input steps up.
#### Diagram Explanation:
- **Voltage Source**: The circle with a
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Consider a parallel plate capacitor with the plate surface area axb and distance between the plates d. A nonconducting slab of a similar size x-bxd with dielectric constant k is completely inserted into the capacitor as shown below. Find the capacitance, charge and energy stored in the system if a battery of 30- V is attached accros the capacitor. Take k = 7.5, a = 11 cm, b = 36 cm, d = 0.3 cm, and x = 6.5 cm. a Ī air The capacitance, C = 565.7706✔ Units pF The echarge, Q = 16.9731 Units nC The energy, U = 2546 x Units nJ K X darrow_forwardThe Ministry of Trade and Industry has approached you to advice on the location of a pineapple processing factory in the Otia District under the 1D1F programme. Whereas some members of the ministry’s project committee want all pineapple-growing areas of the district to be considered fairly for the siting of the factory, others want the choice to be restricted to only the three major towns in the vicinity, namely, Nyamebekyere, Bodumase and Dedeiman. a) Given the information below, compute and graph the centre of gravity (in relation to the three major towns in the district) to enable those arguing for a fair district-wide consideration to visualize where the optimal location would be. Town Coordinates (km) Pineapple Production (Tonnes) X Y Nyamebekyere 95 180 207 Bodumase 240 120 94 Dedeiman 345 370 166arrow_forwardASSIGNMENT: (0,1,1) Problem 1 Given the force field F= 2yi + 2x) + 2zk, (-1,0,0) find a scalar potential o such that F= Vo; () use the potential p to find the work W done by force F in moving from point (-1,0,0) to (0,1,1).arrow_forward
- The following problem is;arrow_forwardPlease answer the questions l have 30min of exam?arrow_forwardB The figure shows a potential well for a particle that can move along an x axis. Four regions of the graph are lettered. Rank those regions according to the magnitude of the force that would act on the particle if it is the region, greatest first. () indicates a tie. U (J) 40 30 20 10 0 2 OC, (A,D), B O A, B, D, C O (A,B,C,D) O C, B, A, D. OD, (B,C), A 4 B 6 7 C 9 12 x (m)arrow_forward
- SOLVE FOR I, Iz amd E Using KIRCHHO F'S RULES E 14V 巧 12= 0-97A a 1052 102arrow_forwardIn the figure ε = 10.4 V, R₁ = 1690 N, R₂ = 3080 N, and R3 = 4780 2. What are the potential differences (in V) (a) VA - VB, (b) VB - VC, (c) Vc-VD, and (d) VA-VC? (a) Number i (b) Number i (c) Number (d) Number i Units V Units R₂ 3 R₂ R₁ Units V Units V V D + + +arrow_forwardGiven: Use the following label: R, = 3.00 Q, R, = 10.0 O, R3 = 5.00 Q, R, = 4.00 Q, and Rs = 6.00 Q. 3.00 N 10.0 N 4.00 N 5.00 N 6.00 N 15.0 V Find: (a) R, (b) I, (c) I,, l2, l3, l4, ls (d) V,, V2, V3, V4, V5 (e) P2, Psarrow_forward
- Consider a solid cylindrical conductor of inner conductor radius 59 cm and outer conductor radius 97 cm with charge Q that is coaxial with a cylindrical shell of negligible thickness. Find the capacitance, in nF, of this cylindrical capacitor if its length is 86 m and the insulator used is mica (εr = 6).arrow_forwardConsider a charged conducting sphere made up of polyethylene (εr = 2.26) with a radius 43 cm. If a charge is uniformly distrubuted over its surface, what is its capacitance, in fF? final answer is in fFarrow_forwardThe capacity of a full cylindrical capacitor of length L with inner radius a and outer radius b, C = (2πϵrϵo)*L / (ln (b / a))is known to be. The capacitor is angularly composed of two insulating regions and these insulating regions are; With ø1 = 2.3 rad and a region with a relative dilutive constant εr1 = 5.6 Regions with relative dilutive constant ø2 = 3.9831 rad r2 = 3.2 The equivalent capacity of this capacitor is how many times the capacitor whose insulator is the space. (ø2 + ø2 = 2π) The gap dielectric constant εo = 8.842 pF / m and capacitor dimensions; L = 20 cm a = 1.5 cm b = 3.4 cmarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios