
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Find the indicated z-scores shown in the attached graph.
First note that the shaded region is an area in between two z-scores. This means that the region is not a cumulative area from the left and to solve requires working instead with regions that are cumulative areas from the left.
Thus, to find the z-scores in this situation, one needs to find the cumulative areas to the left of each unknown z-score.
While either the Standard Normal Table or technology can be used to find the corresponding z-score, in this problem, use the table.
The two values must be approached individually.
First, consider the z-score for the lower 0.4649 to the left of z=0.
The area to the left of this z-score is not given in the problem directly and must be found using the inner areas given.
Note that 0.5 of any Standard Normal Distribution lies to the left of z=0 and that each half is divided into two unequal regions by the unknown z-scores.
The larger region is known from the problem statement to be 0.4649 and the smaller region is the one to the left of the desired z-score.
If the region of this area is known, then the Standard Normal Table can be used to find the z-score.
Using the fact that 0.5 of the distribution lies to the left of z=0, this smaller region is 0.5 − 0.4649 = _________.
Using the cumulative area from the left, locate the closest area in the body of the Standard Normal Table and identify the z-score corresponding to the lower _________.
Round the value to the nearest two decimal places.
The z-score for the lower 0.0351 is _________.
To find the second z-score, find the total cumulative area to the left of the upper z-score.
This is found by summing the three regions to the left of the z-score.
The first two larger regions are given in the problem statement as 0.4649
each.
each.
The third region was found earlier to be _________ when determining the first z-score.
Thus, the sum of these three regions is 0.4649 + 0.4649+ _________ = ?
Now, find the z-score corresponding to _________ in the Standard Normal Table. Round the value to the nearest two decimal places.
z≈ 1.81
Therefore, the z-scores are approximately _________ and __________???
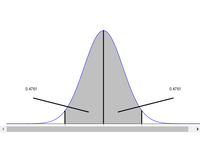
Transcribed Image Text:0.4761
0.4761
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Mr. Palmer, has been teaching beginners how to fix their stroke for the last 10 years. The mean golfing score for all past students who learned with Mr. Palmer is 79. This golfing cycle, he tried a new teaching method using simulations instead of real-world golf. He then had 15 of his students that used his new method take a golfing test. Enter the data into SPSS. Use this dataset to answer this question: did Mr. Palmer’s students perform better on the golfing test using the new method as compared to the traditional teaching technique? 1. From the output, report the test statistic and the probability (obtained p-value, called “sig” in the output). Remember to include degrees of freedom when you report t-values. 2. Will you reject or fail to reject the null based on the SPSS output (Remember to use numbers from the output only to make your statistical conclusion. If you use a critical t, you will get no points.).arrow_forwardA traffic safety company publishes reports about motorcycle fatalities and helmet use. In the first accompanying data table, the distribution shows the proportion of fatalities by location of injury for motorcycle accidents. The second data table shows the location of injury and fatalities for 2061 riders not wearing a helmet. Complete parts (a) and (b) below. Click the icon to view the tables. (a) Does the distribution of fatal injuries for riders not wearing a helmet follow the distribution for all riders? Use α = 0.05 level of significance. What are the null and alternative hypotheses? O A. Ho: The distribution of fatal injuries for riders not wearing a helmet follows the same distribution for all other riders. H₁: The distribution of fatal injuries for riders not wearing a helmet does not follow the same distribution for all other riders. B. Ho: The distribution of fatal injuries for riders not wearing a helmet does not follow the same distribution for all other riders. H₁: The…arrow_forwardLevi-Strauss Co manufactures clothing. The quality control department measures weekly values of different suppliers for the percentage difference of waste between the layout on the computer and the actual waste when the clothing is made (called run-up). The data is in the table, and there are some negative values because sometimes the supplier is able to layout the pattern better than the computer. Do the data show that there is a difference between some of the suppliers? Test at the 1% level. Run-ups for Different Plants Making Levi Strauss Clothing Difference Plant Plant 1 11.9 Plant 1 3.9 -10.6 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 1 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 2 Plant 3 Plant 3 Plant 3 Plant 3 Plant 3 Plant 3 Plant 3…arrow_forward
- Ride services are on the rise, such as Uber and Lyft. You wondered if the recent news reports of crime occurring with these ride services impacted the usage of them, especially with women. You decide to conduct a survey about ride service usage among male and female college students. The results showed that 19 males use ride services and 11 do not. While 12 females use ride services and 18 do not. Calculate the chi-square statistic:arrow_forwardOn average, a sample of n = 36 scores will provide a better estimate of the population mean than a sample of n = 49 scores from the same population.arrow_forwardExplain the t-test as it relates to its application to one samplesarrow_forward
- Suppose that a customer is purchasing a car. He conducts an experiment in which he puts 10 gallons of gas in the car and drives it until it runs out of gas. He conducts this experiment 15 Sample mean for Car 2 x= 245 mi / 10 gal (Type an integer or decimal rounded to one decimal place as needed.) times on each car and records the number of miles driven. Full data set Car 1 Median for Car 1 M= mi / 10 gal (Type an integer or decimal rounded to one decimal place as needed.) 245 242 215 244 220 265 291 160 284 251 169 319 257 306 267 Car 2 Median for Car 2 230 242 M=O mi / 10 gal 206 214 236 256 245 255 241 264 (Type an integer or decimal rounded to one decimal place as needed.) 276 252 250 251 257arrow_forwardThe director of research and development is testing a new drug. She wants to know if there is evidence at the 0.02 level that the drug stays in the system for more than 312 minutes. For a sample of 69 patients, the mean time the drug stayed in the system was 319 minutes. Assume the variance is known to be 400. Step 2 of 5 : Enter the value of the z test statistic. Round your answer to two decimal places.arrow_forwardSee the attached two images for the description and than answer the following questions: Is there an overall positive association or an overall negative association between mean BRFSS score and rank based on the compensating-differentials method? Does the overall association indicate agreement or disagreement between the mean subjective BRFSS score and the ranking based on objective data used in the compensating-differentials method? Are there any outliers? If so, what are the BRFSS scores corresponding to these outliers?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman