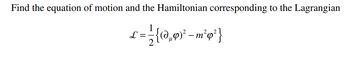
Find the equation of motion and the Hamiltonian corresponding to the Lagrangian L * = {{@, 9)² = m²q²}
Q: For a one-dimensional system with the Hamiltonian H = p2/2 − 1 / (2 q2), show that there is a…
A: Given that,H=p22-12q2D= pq2-HtWe have Liouville's theorem which is,dFdt = ∂F∂t+F, HHere F = DSo in…
Q: (3) Consider the Hamiltonian given as H = +²+Fâ , where each term has a clear physical meaning. 2m 2…
A:
Q: The effective one-body Hamiltonian for a single particle in a central well can be written in…
A: Given Data: The Hamiltonian of the single particle is Hp,q=12mpr2+1r2pθ2+1sin2θpϕ2+Vr To Find:…
Q: Determine the equations describing (2) and (p) for the Hamiltonian given by A = 2 ² 2 + 1/2H (W² 8²…
A:
Q: 420 for a 2D 21 (;2 + 0 r² ) + Suppose that you have the Lagrangian L system in plane polar…
A: Lagrangian The Lagrangian of a system is a mathematical function that is a function of the…
Q: Q4: a) Calculate: (uz|A*|u6). b) If the Hamiltonian of harmonic oscillator defined as H = ħw + A*A…
A:
Q: Show that for a particle in a box of length L and infinite potential outside the box, the function…
A:
Q: Consider a block of mass m on the end of a massless spring of spring constant k and equilibrium…
A: Since you have posted a question that has more than three subparts, we will solve the first three…
Q: Consider a mass m confined to the x axis and subject to a force Fx = kx where k > 0. (a) Write down…
A: If the particle in the given problem has energy E>0, then it can cross the origin. If it has…
Q: Hamiltonian is invariant with the help of an
A:
Q: The Hamiltonian of a two level system is given by - Â = E。[|1X(1| — |2X(2|] + E₁[11X(2| + |2X1|]…
A:
Q: The Longrongion of 1D harmonic oscilator is, () - write Euler-Congronge equation of system? ").…
A:
Q: Question one: Two masses m, M are joined with a light string of length L over a pulley of radius R…
A: Let center of disk be the level of zero potential energy and y1: height of m below the center of…
Q: Employing the power expansion to the solution of the equation of motion, show that for a…
A: Belongs to quantum dynamics and time development in quantum mechanics.
Q: 3. Consider a pendulum of mass m suspended by a massless spring with unextended length b and spring…
A:
Q: the motion, and so is the quantity F(x, p, t) = x − pt/m. (a) Compare {H, F} with ∂F ∂t . Prove…
A: Given,F(x,p,t)=x-ptm(a) As we know,dFdt=F,H+∂F∂tFor free particle H=p22m[H, F]=p22m, x-ptm[H,…
Q: Consider a simple harmonic oscillator with unperturbed Hamiltonian Ho 2m subject to a quartic…
A:
Q: Consider a free real scalar field $(x„), where r, = r, y, z for u = 1,2,3 and r4 = ict, satisfying…
A:
Q: Q 4 For the motion of a projectile write the Lagrangian and the Hamiltonian functions in polar…
A: Let m is the mass of object, then kinetic energy in terms of rectangular coordinate will be,…
Q: Find the gradient and the Laplacian at V(x19, 2) = √(x-1)^-+ (13-b)+(2-c)
A:
Q: Find a Lagrangian corresponding to the following Hamiltonian: H = (P4 + 2P.P. + i)
A:
Q: The Hamiltonian of consisting of a mass' m less sing of length. a simple pendulum attached' to a I…
A:
Q: Problem 3 The Lagrangian of a particle in spherical coordinates is given by 1 L(r, 0, 6; 1, 0, 0) =…
A: Step 1:The Lagrangian given for a particle in spherical coordinates is given in question Step 2: The…
Q: Since the Hamiltonian is obtained using a Legendre transform from the Lagrangian, these two…
A: Lagrangian mechanics Hamiltonian mechanics One second order differential equation Two first…
Q: Let VA), B) be the eigenvectors of the Hamiltonian ♬ of a two-level system Ĥ|VA,B) = EA,B|VA,B) EA>…
A:
Q: In the o field theory, the Lagrangian density is 1 Problem 1 -- 4! Find the equation of motion and…
A:
Q: Verify that Y1 and Y1' are eigenfunctions of the 3D Rigid Rotor Hamiltonian.
A:
Q: Consider a particle of mass m that is constrained to move on the surface of a cone of revolution z =…
A:
Q: Consider if [Lx, A] = 0 and [Ly, A] = 0 where A is an operator and Lx and Ly are components of…
A:
Q: Question 3 If the Lagrange's function for mechanical system is L = ;k (é² + g²(sin 0)² ) + g cos e.…
A: The Lagrangian is L=12kθ˙2+12kϕ˙2sin2θ-gcosθ
Q: The transformation Q = λq, p = λP is canonical while the same transformation with t time dilatation,…
A: The given transformation is canonical when, Q=λq and p=λP. The given transformation is not canonical…
Q: Problem 4: The center of a long frictionless rod is pivoted at the origin, and the rod is forced to…
A:
Q: By applying the methods of the calculus of variations, show that if there is a Lagrangian of the…
A: The hamiltonian principle states that the variation between two points in a conservative system is…
Q: 3. Consider a system described by the Hamiltonian Ĥ = €(−i|0)(1| + i]1)(0]), where {[0), [1)} form…
A: Given that: - The Hamiltonian (H) is given as H = ε(-i|0⟩⟨1|i|1⟩⟨0|)- The eigenenergies of H are ±ε,…
Q: Q3: 0 1 The Hamiltonian is represented by the matrix H = B| 1 0 0 %3D 0 2 Where ß is positive real…
A: given: H=β010100002 Where, β is positive real number
Q: Show that the eigen functions of the Hamiltonian operator are orthogonal and its eigen values are…
A: Hermitian Operators:An operator is said to be Hermitian if it satisfies: A†=ASuppose |am> be the…
Q: Given the Hamiltonian H = p²/2m + a · p + V, with a = a(r) and V = the corresponding Lagrangian. If…
A: Here given that, Hamiltonian is H=p22m+a.p+V......................1Legrangian is the Logendre…
Q: If a particle of mass m is in a potential that is only a function of coordinates, calculate the…
A:
Q: all and the floor are friction-less, the ladder will slide down the wall and along the floor until…
A: A ladder of length L and mass M is leaning against a wall. Assuming the wall and the floor are…
Q: Q2. For a simple pendulum of length t, the angle Obetween rest position and deflected position is…
A: We are given kinetic energy T and potential energy V of the system.
Q: D A The kinetic and potential energies of the vibrating masses are T = mx{+÷mx} v = kxf+k(x2 – x1)²+…
A: The Lagrangian of the system is given by L = T - V Where T = Kinetic energy V = Potential energy…
Q: For the Hamiltonian H= [H₁ [H₁X]]= <²kx. m 2 2m --—--x² 2 + Ex² demonstrate that
A:
Q: Consider a system of two particles, one with spin 1 and the other with spin 1/2. The particles…
A:
Step by step
Solved in 3 steps with 3 images
