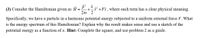
(3) Consider the Hamiltonian given as H = +²+Fâ , where each term has a clear physical meaning. 2m 2 Specifically, we have a particle in a harmonic potential energy subjected to a uniform external force F. What is the energy spectrum of this Hamiltonian? Explain why the result makes sense and use a sketch of the potential energy as a function of x. Hint: Complete the square, and use problem 2 as a guide.

Using the eigenvectors of the quantum harmonic oscillator Hamiltonian, i.e., n), find the matrix element (6|X² P|7).

Need full detailed answer.

5. Consider the two state system with basis |+) which diagonalizes the Pauli matrix 03. Generally the state of the system at time t can be written as |W(t)) = c+(t)|+) + c_(t)|-). (i) For the Hamiltonian of the system, first take H = functions c+(t) given the initial condition that at time t = 0 Eo03. Solve for the coefficient |W(0)) = |-).

The Hamiltonian of an electron of mass m in a constant electric field E in one dimension can be written as Ĥ=+eEx where â and are the position and momentum operators, respectively. With initials conditions (t = 0) = 0 and p(t = 0) = 0, which one of the following gives (t) at time in the Heisenberg picture? You may use the commutator [â,p] = iħ. O a. O b. eEt2 2m O C. e Et O d. -eEt O e. eEt² m pt m