Question
Figure 1.52 shows a spherical shell of charge, of radius a and surface density σ, from which a small circular piece of radius b << a has been removed. What is the direction and magnitude of the field at the midpoint of the aperture? Solve this exercise in three ways: a) direct integration, b) by superposition, and c) using the relationship for a force on a small patch.
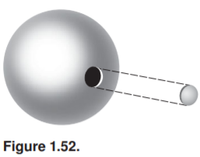
Transcribed Image Text:Figure 1.52.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Problem 2.01. Three plates with surface charge density |o| = 8.85 μC/mm² are stacked on top of each other. The top and bottom plates have charge density to while the center plate has charge density -0. (a) Find the magnitude and direction of the electric field between the plates. (b) Find the magnitude and direction of the electric field above and below the plate stack.arrow_forwardHi, I am having trouble understanding this scenario. Here the charge per unit length on this thin rod shown below is λ. What is the electric field at the point P? Considering the electric field at p is dq = λdx, as a small segment dx of the rod containing the charge . How would I find the net field by integrating over the length of the rod? Any help would be greatly appreciated :)arrow_forwardPre-Class 14.1-14.3: Entropy cem 2 When tossing a certain number of coins, a macrostate is Select all that apply. analogous to the entropy of a system the number of heads obtained analogous to specifying p, T, Eth etc. for a macroscopic system the multiplicity of the states Submit Request Answer Provide Feedback * Previous.arrow_forward
- A cylinder of radius R has a charge density given by p = Po/r where po is a constant, for r R. Find the electric field both inside and outside the cylinder using Gauss' law. 1.arrow_forwardConsider an infinitely long cylinder with radius R. The cylinder is an insulator and it is positively charged, the charge per unit of length is A. (Hint: because it is an insulator you should assume that the charge is spread uniformly across its entire volume). By reflecting on the symmetry of the charge distribution of the system, determine what a) the E-field lines look like around the cylinder. Describe the E-field in words and with a simple sketch. In order to give a complete description of the E-field lines make two sketches: i) one with a side view of the cylinder, ii) one with a cross-sectional view of the cylinder. Make sure to also show the direction of the E-field lines. b) (-- . the figure. Your goal for this part is to properly use Gauss' law to calculate the electric field at point P. Follow the 5 steps below. Consider a point P outside the cylinder, at a distance d from its axis, d > R, as shown inarrow_forwardA thin plastic rod of length L has a positive charge Q uniformly distributed along its length. We willcalculate the exact field due to the rod in the next homework set. In this set, we will approximatethe rod as several point sources and develop the Riemann sum as an intermediate step on the wayto writing an integral.For those aiming at a P rating, you may use L = 3.0m , Q = 17 mC, and y = 0.11m to calculate theanswer numerically first and substitute variables for them only as required in the problem statement.For those aiming at an E rating, leave L, Q and y as variables. Substitute numbers only whererequired in the problem statement, and only as a last steparrow_forward
arrow_back_ios
arrow_forward_ios