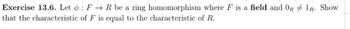
Exercise 13.6. Let : F → R be a ring homomorphism where F is a field and OR 1R. Show that the characteristic of F is equal to the characteristic of R.

Let :312 be defined by ([x]3)=4[x]12 using the same notational convention as in Exercise 9. Prove that is a ring homomorphism. Is (e)=e where e is the unity in 3 and e is the unity in 12?

Prove that if R is a field, then R has no nontrivial ideals.

11. Show that defined by is not a homomorphism.

14. Prove or disprove that is a field if is a field.

Let where is a field and let . Prove that if is irreducible over , then is irreducible over .

[Type here] True or False Label each of the following statements as either true or false. 3. Every integral domain is a field. [Type here]

Suppose that f(x),g(x), and h(x) are polynomials over the field F, each of which has positive degree, and that f(x)=g(x)h(x). Prove that the zeros of f(x) in F consist of the zeros of g(x) in F together with the zeros of h(x) in F.

Let be a field. Prove that if is a zero of then is a zero of

Let R be a commutative ring with unity. Prove that deg(f(x)g(x))degf(x)+degg(x) for all nonzero f(x), g(x) in R[ x ], even if R in not an integral domain.