Edit only the class definition. DO NOT CHANGE the code given under 'main' please. Steps: Additionally implement any Python Magic/Dunder methods such that instances of the class minimally: 1. Support addition, subtraction, equality operations and the built-in abs function 2. Are Iterable i.e., support for loops and star arguments for unpacking into function calls 3. Support a string representation that displays the class name and coordinates stored by the instance: i.e. 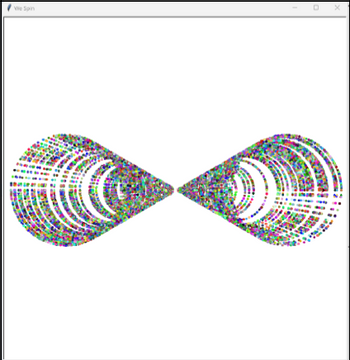for an object initialized as: Vector(0, 3), the string representation should be ‘Vector(0, 3)’ The code given under main tests for each of the program requirements and subsequently uses the turtle module to plot randomly generated points rotated. A screenshot for a sample run of the program is attached.   Template.py: from math import hypot, pi from random import uniform import turtle as t class Vector2D:     ... if __name__ == '__main__':     # Test Vector class     a, b = Vector2D(0, 3), Vector2D(0, -3)     tests = [(str(a), 'Vector2D(0, 3)'),              (repr(a), 'Vector2D(0, 3)'),              (a+b, Vector2D(0, 0)),              (a-b, Vector2D(0, 6)),              (abs(a), hypot(*a)),              (a.dot(b), -9),              (a.scale(3), Vector2D(0, 9)),              (a.direction(), Vector2D(0.0, 1)),              (a.distance(b), 6),              (a.rotate(pi), b),              ([x for x in a], list(a)),              (tuple(a), (0, 3))]     for i, test in enumerate(tests, 1):         assert test[0] == test[1], f'Test {i}: FAIL {test[0]} != {test[1]}'     # All tests passed !!!     # Start drawing     t.setworldcoordinates(-150, -150, 150, 150)     t.title('We Spin')     t.tracer(1000)     t.pu()     # generate 100 points on y-axis between -50 and 50     points = [Vector2D(uniform(-50, 50), 0) for i in range(100)]     # generate 20000 new points by transforming initial points     spin_points = [p.rotate(400/i*pi)+p.scale(2) for p in points for i in range(1, 201)]     # plot spin points     for p in spin_points:         t.goto(*p)         t.pencolor(uniform(0, 1), uniform(0, 1), uniform(0, 1))         t.dot(5)     t.done()

Problem DNA: Subsequence markingA common task in dealing with DNA sequences is searching for particular substrings within longer DNA sequences. Write a function mark_dna that takes as parameters a DNA sequence to search, and a shorter target sequence to find within the longer sequence. Have this function return a new altered sequence that is the original sequence with all non-overlapping occurrences of the target surrounded with the characters >> and <<. Hints: ●  String slicing is useful for looking at multiple characters at once. ●  Remember that you cannot modify the original string directly, you’ll need to build a copy. Start with an empty string and concatenate onto it as you loop. Constraints: ● Don't use the built-in replace string method. All other string methods are permitted. >>> mark_dna('atgcgctagcatg', 'gcg') 'at>>gcg<<ctagcatg' >>> mark_dna('atgcgctagcatg', 'gc')…

python only define the following function: This function must reset the value of every task in a checklist to False.  It accept just one parameter: the checklist object to reset, and it must return the (now modified) checklist object that it was given. Define resetChecklist with 1 parameter Use def to define resetChecklist with 1 parameter   Use a return statement Within the definition of resetChecklist with 1 parameter, use return _in at least one place.   Use any kind of loop Within the definition of resetChecklist with 1 parameter, use any kind of loop in at least one place.

Instructor note: Important Coding Guidelines: Use comments, and whitespaces around operators and assignments. Use line breaks and indent your code. Use naming conventions for variables, functions, methods, and more. This makes it easier to understand the code. Write simple code and do not over complicate the logic. Code exhibits simplicity when it’s well organized, logically minimal, and easily readable. A pedometer treats walking 1 step as walking 2.5 feet. Define a method named feetToSteps that takes a double as a parameter, representing the number of feet walked, and returns an integer that represents the number of steps walked. Then, write a main program that reads the number of feet walked as an input, calls method feetToSteps() with the input as an argument, and outputs the number of steps. Use floating-point arithmetic to perform the conversion. Ex: If the input is: 150.5 the output is: 60 The program must define and call a method:public static int feetToSteps(double…