
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
please do
" for this study, we should use.... (second screenshot) and b & c
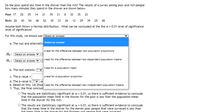
Transcribed Image Text:Do the poor spend less time in the shower than the rich? The results of a survey asking poor and rich people
how many minutes they spend in the shower are shown below.
Poor 17 25
35 14 21 39 21 8 30 35 23
Rich: 28
40
54
46 52 30
33
26 12
29
39
25
48
Assume both follow a Normal distribution. What can be concluded at the the a = 0.01 level of significance
level of significance?
For this study, we should use Select an answer
a. The null and alternativ Select an answer
z-test for the difference between two population proportions
Ho: Select an answer
H: Select an answer
t-test for the difference between two dependent population means
t-test for a population mean
b. The test statistic
c. The p-value =
z-test for a population proportion
d. The p-value is
e. Based on this, we shoul t-test for the difference between two independent population means
f. Thus, the final conclusil
O The results are statistically significant at a = 0.01, so there is sufficient evidence to conclude
that the population mean time in the shower for the poor is less than the population mean
time in the shower for the rich.
O The results are statistically significant at a = 0.01, so there is sufficient evidence to conclude
that the mean time in the shower for the eleven poor people that were surveyed is less than
the mean time in the shower for the thirteen rich neonle that were surveved

Transcribed Image Text:Do the poor spend less time in the shower than the rich? The results of a survey asking poor and rich people
how many minutes they spend in the shower are shown below.
Poor 17
25
35
14
21
39 21 8 30 35 23
Rich: 28
40
54
46
52
30 33
26 12
29
39
25
48
Assume both follow a Normal distribution. What can be concluded at the the a = 0.01 level of significance
level of significance?
For this study, we should use Select an answer
a. The null and alternative hypotheses would be:
Ho: Select an answer
Select an answer V Select an answer
(please enter a decimal)
Hj:
Select an answer V Select an answer V Select an answer
(Please enter a decimal)
b. The test statistic
(please show your answer to 3 decimal places.)
c. The p-value =
d. The p-value is ?Va
e. Based on this, we should Select an answer
f. Thus, the final conclusion is that ...
O The results are statistically significant at a = 0.01, so there is sufficient evidence to conclude
(Please show your answer to 4 decimal places.)
) the null hypothesis.
that the population mean time in the shower for the poor is less than the population mean
time in the shower for the rich.
O The results are statistically significant at a = 0.01, so there is sufficient evidence to conclude
that the mean time in the shower for the eleven poor people that were surveyed is less than
the mean time in the shower for the thirteen rich people that were surveyed.
O The results are statistically insignificant at a = 0.01, so there is statistically significant
evidence to conclude that the population mean time in the shower for the poor is equal to the
population mean time in the shower for the rich.
O The results are statistically insignificant at a = 0.01, so there is insufficient evidence to
conclude that the population mean time in the shower for the poor is less than the population
mean time in the shower for the rich.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Mr. Palmer, has been teaching beginners how to fix their stroke for the last 10 years. The mean golfing score for all past students who learned with Mr. Palmer is 79. This golfing cycle, he tried a new teaching method using simulations instead of real-world golf. He then had 15 of his students that used his new method take a golfing test. Enter the data into SPSS. Use this dataset to answer this question: did Mr. Palmer’s students perform better on the golfing test using the new method as compared to the traditional teaching technique? 1. From the output, report the test statistic and the probability (obtained p-value, called “sig” in the output). Remember to include degrees of freedom when you report t-values. 2. Will you reject or fail to reject the null based on the SPSS output (Remember to use numbers from the output only to make your statistical conclusion. If you use a critical t, you will get no points.).arrow_forwardWrite an example of a research study that would be most appropriate for a within subjects ANOVAarrow_forwardPlease help me with the following sections: d, e, f, g, h and i Thank you!arrow_forward
- I am doing a case study for statistics and I have to do a report with it. What do I include on the report? Do I just add bar graphs scatter plots and histograms? can I add multiple regression tables to the report? What should I not include?arrow_forwardGive an example of how a nonrepresentative sample can severely affect a regression analysis.arrow_forwardThe study sorted PIR data into three categories: Use the graphs to estimate the following information from the study. You may wish to record your responses for use in later questions. Part A: The total number of obese men is about million. Part B: The total number of obese women is about million. Part C: The number of obese men with PIR<130% is about million. Part D: The number of obese women with PIR<130% is about million.arrow_forward
- Why is Data literacy important when evaluating sources from a study?arrow_forwardExplain the t-test as it relates to its application to one samplesarrow_forwardIf you found a strong positive correlation between the number of hours learners spent reading their textbooks and their quiz scores, you could conclude that reading the textbook caused better performancesarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman