
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
Draw the combinational logic circuit of the following propositions and also draw its simplified circuit (if possible) by applying logical equivalence.
PS: I REALLY NEED THE COMBINATIONAL LOGIC CIRCUIT OF THESE PROPOSITIONS
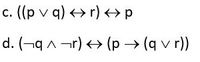
Transcribed Image Text:c. ((p v q) > r) p
С.
d. (-q A ¬r) <> (p → (q v r))
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Part 1: Choose two of the proofs below and use one of the indirect proof techniques (reductio ad absurdum or conditional proof) presented in Chapter 8 to demonstrate the validity of the arguments. The proofs below may use any of the rules of inference or replacement rules given in Chapter 8. 1.(G • P) → K, E → Z, ~P → ~ Z, G → (E v L), therefore, (G • ~L) → K 2.(S v T) ↔ ~E, S → (F • ~G), A → W, T → ~W, therefore, (~E • A) → ~G 3.(S v T) v (U v W), therefore, (U v T) v (S v W) 4.~Q → (L → F), Q → ~A, F → B, L, therefore, ~A v B 5.~S → (F → L), F → (L → P), therefore, ~S → (F → P) Part 2: Below are basic arguments in English. Choose two arguments and translate those argument into the symbolism of predicate logic. You do not need to do a proof. Every fetus has an immortal soul. A thing has an immortal soul only if it has a right to life. Hence, every fetus has a right to life. (Fx = x is a fetus, Sx = x has an immortal soul, Rx = x has a right to life). Some wars are just. No war of…arrow_forwardTranslate the following First Order Logic in English sentence. (Attached)arrow_forward3. Express the following English sentences using propositional functions, quantifiers and logical connections. (a) Someone in the class is helped by everyone in the class. (b) There is a hard working student in the class who has not been helped by any student in class. (c) For everyone in the class, someone who is smart has helped him/her. SO (d) There are two people in the class who have not helped each other. (e) There is a hard working student in the class who is helped by every smart student in class. (f) There are some companies that hire only hard working students.arrow_forward
- discrete math... 6. Use the laws of propositional logic to show that: a). (p ∨ q) ∧ ¬q ≡ ¬p ∧ q b). (¬ p ∨ q) → (p ∧ q) ≡ P c). p ∧ (¬ p → q) ≡ P (Note not use Truth Table)arrow_forwardWhat is the difference between ‘⊢’ and ‘⊨’. In giving your answer, briefly describe the two (equivalent) notions of validity we have given for truth-functional logic. (2-4 sentencesarrow_forwardProve the following proposition to be a tautology by constructing a proof for the following theorem within the system of sentential logic: ~(P ≡ Q) ⊃ (P ≡ ~Q)arrow_forward
- Could you complete question 3 a and b. Please write the diagram and truth table neatly. Thanks!arrow_forwardProve the following predicate logic statements valid or invalid: A) ∀x(A(x) → B(x)) ∧ ∀x(A(x) ∨ ¬C(x)) ∧ ∃x(¬B(x)) → ¬∃x(¬A(x) ∧ ¬B(x) ∧ ¬C(x)) B) ∀x(A(x) → B(x)) ∧ ∃x(A(x) ∨ B(x)) → ∃x(A(x) ∧ B(x))arrow_forward1. State the deduction theorem in logic 2. If A ⊨ B, then A, C ⊨ B. What is this feature of entailment known as?arrow_forward
- Consider a proof system P in the style of box-proof which only have one logical connective A. The system only has one rule given by: [X] Y YAX Here, X and Y can represent any formula. Tick each that applies. In the proof system P it is possible to derive the formula ((AAC)AB)AA In the proof system P it is possible to derive AA(AA A) In the proof system P it is possible to derive the formula AAA In the proof system P it is possible to derive (AAA)^ A In the proof system P it is not possible to derive (AA B)A(BAA)arrow_forwardTranslate each of these nested quantifications into an English statement that expresses a mathematicalfact. The domain in each case consists of all real numbers.a) ∃x∀y(x + y = y) b) ∀x∀y (((x ≥ 0) ∧ (y < 0)) → (x − y > 0))c) ∃x∃y(((x ≤ 0) ∧ (y ≤ 0)) ∧ (x − y > 0))d) ∀x∀y((x ≠ 0) ∧ (y ≠ 0) ↔ (xy ≠ 0))arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education