Question
Determine the gravitational field at mass A. The radius of masses A and C is 50 cm while the radius of mass B is 75 cm.
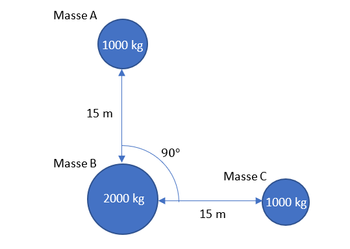
Transcribed Image Text:Masse A
1000 kg
15 m
Masse B
2000 kg
90°
Masse C
15 m
1000 kg
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 1 images

Knowledge Booster
Similar questions
- You have a super high-tech spacecraft travelling through space that gets caught in a circular orbit around a mysterious object of mass 10 times that of the Sun and a radius of 30km. Your team decides to observe the behavior of this object but due to the heat that it's giving off, it is required that your satellite obtain a circular orbit of at least r = 5.3e5km to be considered 'safe'. You are currently in a circular orbit with r = 4.1e5km. What is the minimum delta-v required to reach the safe orbitarrow_forwardThe mean diameters of planets A and B are 9.3 × 103 km and 1.8 × 104 km, respectively. The ratio of the mass of planet A to that of planet B is 0.88. (a) What is the ratio of the mean density of A to that of B? (b) What is the ratio of the gravitational acceleration on A to that on B? (c) What is the ratio of escape speed on A to that on B?arrow_forwardWhat is the gravitational field intensity at a distance of 8.4 x 107 m from the centre of Earth?arrow_forward
- The free-fall acceleration on the surface of Neptune is about one and one-half times that on the surface of the Earth. The radius of Neptune is about 3.50 RE (RE = Earth's radius = 6.4 *106 m). Find the ratio of their average densities, ?Neptune/?Earth.arrow_forwardA meteoroid is moving towards a planet. It has mass m = 0.18×109 kg and speed v1 = 3.8×107 m/s at distance R1 = 1.6×107 m from the center of the planet. The radius of the planet is R = 0.26×107 m. The mass of the planet is M = 10×1025 kg. There is no air around the planet. a)Enter an expression for the total energy E of the meteoroid at R, the surface of the planet, in terms of defined quantities and v, the meteoroid’s speed when it reaches the planet’s surface. b)Enter an expression for v, the meteoroid’s speed at the planet’s surface, in terms of G, M, v1, R1, and R. c)Calculate the value of v in meters per second.arrow_forwardSally and Sam are in a spaceship that comes to within 14,000 km of the asteroid Ceres. Determine the force Sally experiences due to the presence of the asteroid. The mass of the asteroid is 8.7 x 1020 kg and the mass of Sally is 79 kg. For calculation purposes assume the two objects to be point masses. Narrow_forward
- A very dense UFS (Unidentified Flying Sphere) has radius 1370_m and acceleration due to gravity 9.4 m/s at its surface. Find the mass of the sphere. (Note that the mass is given in exagrams or Eg, and 1 Eg = 1018 grams.) 310.6 Eg 252.4 Eg 276.5 Eg 264.5_Eg 290 Eg 300.4 Eg А. D. В. Е. С. F.arrow_forwardThe mass of the Sun is 2 × 10³⁰0 kg, and the mass of Mercury is 3.3 × 10²³ kg. The distance from the center of mass of the Sun to the center of mass of Mercury is 4.8 x 10¹⁰ m. a. Calculate the magnitude of the gravitational force exerted by the Sun on Mercury. b. What is the magnitude of the gravitational force exerted by Mercury on the Sun?arrow_forwardTwo Planets, A and B, are orbiting a common star. Planet A is twice as massive as planet B and orbits at twice the distance from the star. Planet A orbits the star with a 'year' that is 240 days long. Assuming that both planets have the same average density, how long (in days) is a year on planet B?arrow_forward
- The radius Rh of a black hole is the radius of a mathematical sphere, called the event horizon, that is centered on the black hole. Information from events inside the event horizon cannot reach the outside world. According to Einstein's general theory of relativity, Rh = 2GM/c2, where M is the mass of the black hole and c is the speed of light. Suppose that you wish to study a black hole near it, at a radial distance of 48Rh. However, you do not want the difference in gravitational acceleration between your feet and your head to exceed 10 m/s2 when you are feet down (or head down) toward the black hole. (a) Take your height to be 1.5 m. What is the limit to the mass of the black hole you can tolerate at the given radial distance? Give the ratio of this mass to the mass MS of our Sun.arrow_forwardSuppose two worlds, each having mass M and radius R, coalesce into a single world. Due to gravitational contraction, the combined world has a radius of only 3/4R. What is the average density of the combined world as a multiple of ρ0, the average density of the original two worlds?arrow_forwardA meteoroid is moving towards a planet. It has mass m = 0.18×109 kg and speed v1 = 3.8×107 m/s at distance R1 = 1.6×107 m from the center of the planet. The radius of the planet is R = 0.26×107 m. The mass of the planet is M = 10×1025 kg. There is no air around the planet. a)Enter an expression for the total energy E of the meteoroid at R, the surface of the planet, in terms of defined quantities and v, the meteoroid’s speed when it reaches the planet’s surface. b)Enter an expression for v, the meteoroid’s speed at the planet’s surface, in terms of G, M, v1, R1, and R. c)Calculate the value of v in meters per second.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios