
Concept explainers
Write a while loop that lets the user enter a number. The number should be multiplied
by 10, and the result assigned to a variable named product. The loop should iterate as
long as product is less than 100.
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

I would like for the code in the attached image turned into a flow chart.
Thanks in advance!
![```python
import math
def isSquare(n):
sr = (int) (math.sqrt(n))
return (sr * sr == n)
def printPrimeAndFib(n):
prime =[True] * (n + 1)
p = 2
while(p * p <= n):
if (prime[p] == True):
for i in range(p * 2, n + 1, p):
prime[i] = False
p = p + 1
for i in range(2, n + 1):
if (prime[i] and (isSquare(5 * i * i + 4) > 0 or isSquare(5 * i * i - 4) > 0)):
print(i , " ",end="")
n = 233
printPrimeAndFib(n);
```
### Description
This Python script includes functions designed to identify and print numbers that are both prime and Fibonacci up to a given number `n`.
#### Functions
1. **isSquare(n)**
- Determines if a number `n` is a perfect square.
- Returns `True` if `n` is a perfect square, otherwise `False`.
2. **printPrimeAndFib(n)**
- Identifies prime numbers using the Sieve of Eratosthenes.
- Checks for Fibonacci numbers using the property that a number `x` is a Fibonacci number if one (or both) of `(5*x*x + 4)` or `(5*x*x - 4)` is a perfect square.
- Prints numbers that are both prime and Fibonacci within the range `2` to `n`.
#### Example
- Sets `n = 233` and calls `printPrimeAndFib(n)` to print all numbers up to 233 that are both prime and Fibonacci.
This script serves as an educational example for applying mathematical properties and concepts to solve a problem involving prime and Fibonacci numbers.](https://content.bartleby.com/qna-images/question/a7e1b932-69d6-4780-b755-a77130ed504e/70f36788-d69e-4640-b0a1-86eabd6da7ce/iyw5k8e_thumbnail.png)
Design a loop (pick one you would like to use) that lets a user enter a number. Have the
*Does the flow chart in the attached image describe what is required in the above paragraph?*
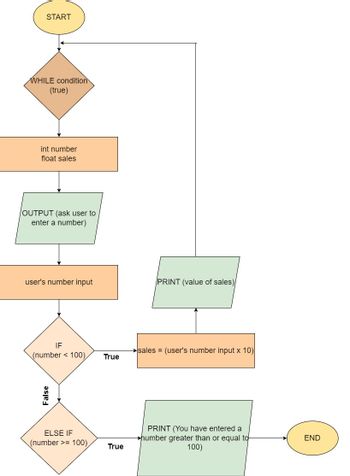
Design a loop (pick one you would like to use) that lets a user enter a number. Have the
I would like for the code in the attached image turned into a flow chart.
Thanks in advance!
![```python
import math
def isSquare(n):
sr = (int) (math.sqrt(n))
return (sr * sr == n)
def printPrimeAndFib(n):
prime =[True] * (n + 1)
p = 2
while(p * p <= n):
if (prime[p] == True):
for i in range(p * 2, n + 1, p):
prime[i] = False
p = p + 1
for i in range(2, n + 1):
if (prime[i] and (isSquare(5 * i * i + 4) > 0 or isSquare(5 * i * i - 4) > 0)):
print(i , " ",end="")
n = 233
printPrimeAndFib(n);
```
### Description
This Python script includes functions designed to identify and print numbers that are both prime and Fibonacci up to a given number `n`.
#### Functions
1. **isSquare(n)**
- Determines if a number `n` is a perfect square.
- Returns `True` if `n` is a perfect square, otherwise `False`.
2. **printPrimeAndFib(n)**
- Identifies prime numbers using the Sieve of Eratosthenes.
- Checks for Fibonacci numbers using the property that a number `x` is a Fibonacci number if one (or both) of `(5*x*x + 4)` or `(5*x*x - 4)` is a perfect square.
- Prints numbers that are both prime and Fibonacci within the range `2` to `n`.
#### Example
- Sets `n = 233` and calls `printPrimeAndFib(n)` to print all numbers up to 233 that are both prime and Fibonacci.
This script serves as an educational example for applying mathematical properties and concepts to solve a problem involving prime and Fibonacci numbers.](https://content.bartleby.com/qna-images/question/a7e1b932-69d6-4780-b755-a77130ed504e/70f36788-d69e-4640-b0a1-86eabd6da7ce/iyw5k8e_thumbnail.png)
Design a loop (pick one you would like to use) that lets a user enter a number. Have the
*Does the flow chart in the attached image describe what is required in the above paragraph?*

Design a loop (pick one you would like to use) that lets a user enter a number. Have the
- A for loop is a ______ loop. Select one: a. Limit-controlled b. Function-controlled c. Range-controlled d. Count-controlledarrow_forwardThe following for loop should be converted to a while loop: for a number in the range(90,9,-9): create a printoutarrow_forwardTrue or False When a variable is declared in the initialization expression of a for loop, the scope of the variable is limited to the loop.arrow_forward
- The main difference between using do/while loop and while loop is that while loop executes the code block once then it checked if the condition is true so it will repeat the loop. True Falsearrow_forwardThe following loop displays _____. for (int i = 1; i <= 10; i+=2) { System.out.print(i + " "); i++; } a)1 2 3 4 5 6 7 8 9 b)1 2 3 4 5 6 7 8 9 10 c)1 3 5 7 9 d)3 5 7 9 11arrow_forward* True Or False A break statement will leave the outer loop. True O False Oarrow_forward
- True or False: When asking user for data, we can always turn an algorithm that uses a user-confirmation loop into one that uses a sentinel loop. Select one: a. False b. Truearrow_forwardIs it real or not? A variable's scope is limited to the for loop when it is specified in the initialization phrase.arrow_forward3 نقاط * To generate a loop that runs 10 times, one of the following statements -:must be used for x = 1:10 O for x = 0:10 O for x = 10 O for x = 10:1 O for x = 10:0 Oarrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





